
活动:终边落在y轴上,应分y轴的正方向与y轴的负方向两个.
学生很容易分别写出所有与90°,270°的终边相同的角构成集合,这时应启发引导学生进一步思考:能否化简这两个式子,用一个式子表示出来.
让学生观察、讨论、思考,并逐渐形成共识,教师再规范地板书出来.并强调数学的简捷性.在数学表达式子不唯一的情况下,注意采用简约的形式.
解:在0°—360°范围内,终边在y轴上的角有两个,
即90°和270°角,如图4.
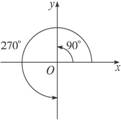
图4
因此,所有与90°的终边相同的角构成集合
S1={β|β=90°+k·360°,k∈Z}.
而所有与270°角的终边相同的角构成集合
S2={β|β=270°+k·360°,k∈Z}.
于是,终边在y轴上的角的集合
S=S1∪S2
={β|β=90°+2k·180°,k∈Z}∪{β|β=90°+180°+2k·180°,k∈Z}
={β|β=90°+2k·180°,k∈Z}∪{β|β=90°+(2k+1)·180°,k∈Z}
={β|β=90°+n·180°,n∈Z}.
点评:本例是让学生理解终边在坐标轴上的角的表示.教学中,应引导学生体会用集合表示终边相同的角时,表示方法不唯一,要注意采用简约的形式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 (2009•奉贤区一模)已知函数f(x)=
(2009•奉贤区一模)已知函数f(x)=| 6 |
| x2+1 |
| 6 |
| x2+1 |
查看答案和解析>>
科目:高中数学 来源:2004全国各省市高考模拟试题汇编(天利38套)·数学 题型:044
已知f(x)是定义在(-∞,+∞)上且以2为周期的函数,当x∈[0,2]时,其解析式为f(x)=|x-1|.
(Ⅰ)作出f(x)在(-∞,+∞)上的图像;(注:请将图像画在模拟答题卡所给出的直角坐标系中.)
(Ⅱ)写出f(x)在[2k,2k+2](k∈Z)上的解析式,并证明f(x)是偶函数.
查看答案和解析>>
科目:高中数学 来源:学习高手必修二数学苏教版 苏教版 题型:022
在空间直角坐标系中,写出点P(x,y,z)的对称点的坐标.
(1)关于x轴的对称点是P1________;
(2)关于y轴的对称点是P2________;
(3)关于z轴的对称点是P3________;
(4)关于原点的对称点是P4________;
(5)关于xOy坐标平面的对称点是P5________;
(6)关于yOz坐标平面的对称点是P6________;
(7)关于zOx坐标平面的对称点是P7________.
查看答案和解析>>
科目:高中数学 来源:上海市十三校2012届高三第二次联考数学理科试题 题型:044
现代城市大多是棋盘式布局(如北京道路几乎都是东西和南北走向).在这样的城市中,我们说的两点间的距离往往不是指两点间的直线距离(位移),而是实际路程(如图).在直角坐标平面内,我们定义A(x1,y1),B(x2,y2)两点间的“直角距离”为:D(AB)=|x1-x2|+|y1-y2|.

(1)在平面直角坐标系中,写出所有满足到原点的“直角距离”为2的“格点”的坐标.(格点指横、纵坐标均为整数的点)
(2)求到两定点F1、F2的“直角距离”和为定值2a(a>0)的动点轨迹方程,并在直角坐标系内作出该动点的轨迹.
①F1(-1,0),F2(1,0),a=2;
②F1(-1,-1),F2(1,1),a=2;
③F1(-1,-1),F2(1,1),a=4.
(3)写出同时满足以下两个条件的“格点”的坐标,并说明理由(格点指横、纵坐标均为整数的点).
①到A(-1,-1),B(1,1)两点“直角距离”相等;
②到C(-2,-2),D(2,2)两点“直角距离”和最小.

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知函数
已知函数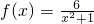
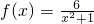 大致图象.
大致图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com