
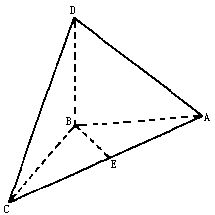
如图所示,空间四边形ABCD中,AB,BC,BD两两垂直,AB=BC=2,E为AC的中点,异面直线AD与BE所成角的大小为arccos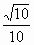 ,求二面角D-AC-B的大小.
,求二面角D-AC-B的大小.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
如图所示,已知圆的方程是(x-1)2+y2=1,四边形PABQ为该圆内接梯形,底边AB为圆的直径且在x轴上,以A,B为焦点的椭圆C过P,Q两点.
(1)若直线QP与椭圆C的右准线相交于点M,求点M的轨迹方程;
(2)当梯形PABQ周长最大时,求椭圆C的方程.

查看答案和解析>>
科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
如图所示,在直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=2a,BB1=3a,D是A1C1的中点,E是B1C的中点.
(1)求cos( ,
, ).
).
(2)在线段AA1上是否存在点F,使CF⊥平面B1DF?若存在,求出| |;若不存在,请说明理由.
|;若不存在,请说明理由.

查看答案和解析>>
科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
如图所示,椭圆方程为 +
+ =1(a>b>0),A,P,F分别为左顶点,上顶点,右焦点,E为x轴正方向上一点,且|
=1(a>b>0),A,P,F分别为左顶点,上顶点,右焦点,E为x轴正方向上一点,且| |,|
|,| |,|
|,| |成等比数列.又点N满足
|成等比数列.又点N满足 =
= (
( +
+ ),PF的延长线与椭圆的交点为Q,过Q与x轴平行的直线与PN的延长线交于M.
),PF的延长线与椭圆的交点为Q,过Q与x轴平行的直线与PN的延长线交于M.
(1)求证: ·
· =
= ·
· .
.
(2)若 =2
=2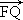 ,且|
,且| |=
|= ,求椭圆方程.
,求椭圆方程.

查看答案和解析>>
科目:高中数学 来源:2004年高考教材全程总复习试卷·数学 题型:044
如图所示,某电子器件是由三个电阻组成的回路,其中共有六个焊接点A,B,C,D,E,F,如果某个焊接点脱落,整个电路就会不通.
(1)求因焊接点脱落致使电路不通的所有不同的脱落种数.
(2)每个焊接点脱落的概率均是 ,现在发现电路不通了,那么至少有两个焊接点脱落的概率是多少?
,现在发现电路不通了,那么至少有两个焊接点脱落的概率是多少?

查看答案和解析>>
科目:高中数学 来源:2007届潜山中学理复(一、二)数学周考试卷 题型:044
| |||||||||||
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com