
分析 由条件求得cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,从而求得<$\overrightarrow{a}$,$\overrightarrow{b}$>的值.
解答 解:已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,|$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{7}$,∴${\overrightarrow{a}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=4-2×2×3cos<$\overrightarrow{a}$,$\overrightarrow{b}$>+9=7,
则cos<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{1}{2}$,∴<$\overrightarrow{a}$,$\overrightarrow{b}$>=$\frac{π}{3}$,
故答案为:$\frac{π}{3}$.
点评 本题主要考查两个向量的数量积的定义,根据三角函数的值求角,属于基础题.


 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 3:2 | B. | 2:3 | C. | 3:7 | D. | 7:2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0] | B. | (-3,0) | C. | [-3,0] | D. | [-3,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{7}}}{2}$ | B. | $\frac{7}{2}$ | C. | $\frac{5}{2}$ | D. | $\frac{{\sqrt{7}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
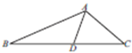 如图,在△ABC中,AB=3,AC=2,BC=4,点D在边BC上,∠BAD=30°,则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$.
如图,在△ABC中,AB=3,AC=2,BC=4,点D在边BC上,∠BAD=30°,则sin∠CAD的值为$\frac{3\sqrt{5}+1}{8}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com