
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
科目:高中数学 来源: 题型:
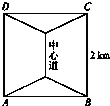 某乡有A、B、C、D四个村庄,恰好座落在边长为2km的正方形顶点上,为发展经济,当地政府决定建立一个使得任何两个村庄都有通道的路网,道路网由一条中心道及四条支线组成,要求四条支道的长度相等.(如图所示)
某乡有A、B、C、D四个村庄,恰好座落在边长为2km的正方形顶点上,为发展经济,当地政府决定建立一个使得任何两个村庄都有通道的路网,道路网由一条中心道及四条支线组成,要求四条支道的长度相等.(如图所示)查看答案和解析>>
科目:高中数学 来源: 题型:
| A、x2+y-1=0 | ||
B、|x|-
| ||
| C、x2+y2-x-|x|-1=0 | ||
| D、3x2-xy+1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| x |
| A、定值1 |
| B、定值2 |
| C、定值4 |
| D、随点P的位置变化而变化 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、2 | ||
| B、1 | ||
| C、e | ||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com