
【题目】某种产品的广告费用支出![]() 与销售额
与销售额![]() 之间有如下的对应数据:
之间有如下的对应数据:
| 2 | 4 | 5 | 6 | 8 |
| 30 | 40 | 60 | 50 | 70 |
(1)画出散点图;并说明销售额y与广告费用支出x之间是正相关还是负相关?
(2)请根据上表提供的数据,求回归直线方程![]() ;
;
(3)据此估计广告费用为10时,销售收入![]() 的值.
的值.
(参考公式: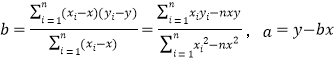 ,).
,).
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]()
![]() (t+1)lnx,,其中t∈R.
(t+1)lnx,,其中t∈R.
(1)若t=1,求证:当x>1时,f(x)>0成立;
(2)若t>![]() ,判断函数g(x)=x[f(x)+t+1]的零点的个数.
,判断函数g(x)=x[f(x)+t+1]的零点的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() 对
对![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(2)是否存在整数![]() ,使得函数
,使得函数![]() 在区间
在区间![]() 上存在极小值,若存在,求出所有整数
上存在极小值,若存在,求出所有整数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,![]() ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
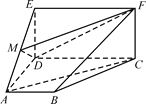
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某企业生产的产品中抽取1000件测量这些产品的一项质量指标值,由测量结果得到频率分布直方图如图所示.
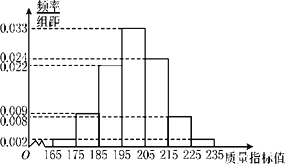
(Ⅰ)求这1000件产品质量指标值的样本平均数![]() 和样本方差s2(同一组数据用该区间的中点值作代表).
和样本方差s2(同一组数据用该区间的中点值作代表).
(Ⅱ)由频率分布直方图可以认为这种产品的质量指标值Z服从正态分布N(μ,δ2),其中μ近似为样本平均数![]() ,δ2近似为样本方差s2.
,δ2近似为样本方差s2.
![]() 利用该正态分布,求P(175.6<Z<224.4);
利用该正态分布,求P(175.6<Z<224.4);
②某用户从该企业购买了100件这种产品,估计其中质量指标值位于区间(175.6,224.4)的产品件数.(精确到个位)
附: ![]() ≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,
≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,
P(μ-2δ<Z<μ+2δ)=0.9544
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在
定义在![]() 上的奇函数,
上的奇函数, ![]() 的最大值为
的最大值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)关于![]() 的方程
的方程![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若存在![]() ,不等式
,不等式![]() 成立,请同学们探究实数
成立,请同学们探究实数![]() 的所有可能取值.
的所有可能取值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com