
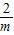 )]>3m,又因为m<0,分x=1和x≠1,当x≠1时g(t)=t-
)]>3m,又因为m<0,分x=1和x≠1,当x≠1时g(t)=t- ,求出g(t)的最小值.要使
,求出g(t)的最小值.要使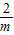 <(x-1)-
<(x-1)-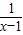 恒成立即要g(t)的最小值>
恒成立即要g(t)的最小值>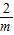 ,解出不等式的解集求出m的范围.
,解出不等式的解集求出m的范围.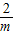 )]
)]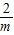 ,当x变化时f(x)与f'(x)的变化如下表:
,当x变化时f(x)与f'(x)的变化如下表: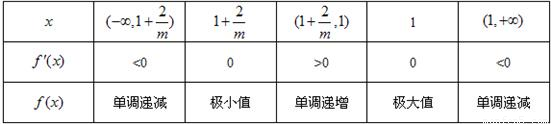
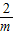 )单调递减,在(1+
)单调递减,在(1+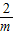 ,1)单调递增,在(1,+∞)单调递减.
,1)单调递增,在(1,+∞)单调递减.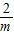 )]>3m,
)]>3m,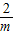 )]<1.(*)
)]<1.(*)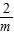 <(x-1)-
<(x-1)-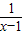 .
. ,
,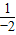 =-
=- .
.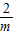 <-
<- ⇒-
⇒- <m,又m<0.∴-
<m,又m<0.∴- <m<0.
<m<0. <m<0.
<m<0.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| e |
| 1 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com