
设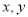 是两个实数,则“
是两个实数,则“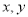 中至少有一个数大于1”是“
中至少有一个数大于1”是“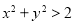 ”成立的( )
”成立的( )
A.充分非必要条件 B.必要非充分条件
C.充分必要条件 D.既非充分又非必要条件
D
【解析】
试题分析:若x=1.5,y=0.5则 不成立所以“
不成立所以“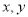 中至少有一个数大于1”,不能得到“
中至少有一个数大于1”,不能得到“ ”.故充分性不成立;令x=-2,y=-2,则
”.故充分性不成立;令x=-2,y=-2,则 成立,“
成立,“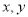 中至少有一个数大于1”不成立.所以必要性不成立.故选D.
中至少有一个数大于1”不成立.所以必要性不成立.故选D.
考点:充要条件
考点分析: 考点1:必要条件、充分条件与充要条件的判断 【知识点的认识】正确理解和判断充分条件、必要条件、充要条件和非充分非必要以及原命题、逆命题否命题、逆否命题的概念是本节的重点;掌握逻辑推理能力和语言互译能力,对充要条件概念本质的把握是本节的难点.

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年陕西省宝鸡市九校高三联合检测理科数学试卷(解析版) 题型:选择题
已知命题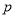 :存在
:存在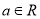 ,曲线
,曲线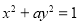 为双曲线;命题
为双曲线;命题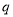 :
: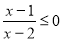 的解集是
的解集是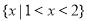 .给出下列结论中正确的有( )
.给出下列结论中正确的有( )
①命题“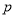 且
且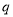 ”是真命题;
”是真命题;
②命题“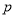 且(
且(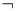
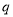 )”是真命题;
)”是真命题;
③命题“(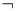
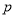 )或
)或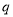 ”为真命题;
”为真命题;
④命题“(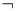
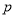 )或(
)或(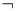
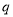 )”是真命题.
)”是真命题.
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试文科数学试卷(解析版) 题型:解答题
(12分)已知函数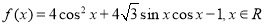 .
.
(1)求函数的最小正周期、最大值及取最大值时自变量的取值集合;
(2)在△ABC中,角A,B,C的对边分别是a,b,c;若a,b,c成等比数列,且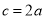 ,求
,求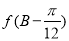 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试文科数学试卷(解析版) 题型:选择题
已知双曲线的两个焦点分别为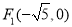 ,
,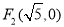 ,P是双曲线上的一点,
,P是双曲线上的一点,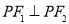 且
且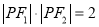 ,则双曲线方程是( )
,则双曲线方程是( )
A.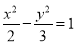 B.
B.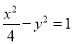 C.
C.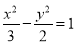 D.
D.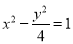
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试理科数学试卷(解析版) 题型:解答题
设函数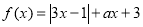 .
.
(1)若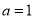 时,解不等式
时,解不等式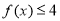 ;
;
(2)若函数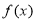 有最小值,求a的取值范围.
有最小值,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年江西省吉安市高三上学期第二次阶段考试理科数学试卷(解析版) 题型:解答题
已知数列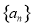 的前n项和为
的前n项和为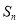 ,
,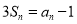
 .
.
(1)求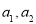 ;
;
(2)求证:数列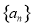 是等比数列;
是等比数列;
(3)求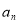 .
.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年河北省唐山市高三第一次模拟考试文科数学试卷(解析版) 题型:解答题
(本小题满分10分)选修4-5:不等式选讲
已知函数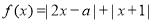 .
.
(Ⅰ)当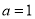 时,解不等式
时,解不等式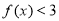 ;
;
(Ⅱ)若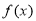 的最小值为1,求a的值.
的最小值为1,求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com