
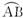
图2-16
A.△AED∽△BEC B.∠AEB=90°
C.∠BDA=45° D.图中共有2对全等三角形
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
 某市教育局规定:初中升学须进行体育考试,总分30分,成绩计入初中毕业升学考试总分,还将作为初中毕业生综合素质评价“运动和健康”维度的实证材料.为了解九年级学生的体育素质,某校从九年级的六个班级共420名学生中按分层抽样抽取60名学生进行体育素质测试.
某市教育局规定:初中升学须进行体育考试,总分30分,成绩计入初中毕业升学考试总分,还将作为初中毕业生综合素质评价“运动和健康”维度的实证材料.为了解九年级学生的体育素质,某校从九年级的六个班级共420名学生中按分层抽样抽取60名学生进行体育素质测试.查看答案和解析>>
科目:高中数学 来源: 题型:
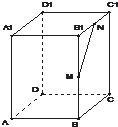 (2013•浦东新区二模)如图,已知正四棱柱ABCD-A1B1C1D1的底面边长是2,体积是16,M,N分别是棱BB1、B1C1的中点.
(2013•浦东新区二模)如图,已知正四棱柱ABCD-A1B1C1D1的底面边长是2,体积是16,M,N分别是棱BB1、B1C1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:
(06年山东卷理)下列四个命题中,真命题的序号有 (写出所有真命题的序号).
①将函数y=![]() 的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=
的图象按向量y=(-1,0)平移,得到的图象对应的函数表达式为y=![]()
②圆x2+y2+4x-2y+1=0与直线y=![]() 相交,所得弦长为2
相交,所得弦长为2
③若sin(![]() +
+![]() )=
)=![]() ,sin(
,sin(![]() -
-![]() )=
)=![]() ,则tan
,则tan![]() cot
cot![]() =5
=5
④如图,已知正方体ABCD- A1B1C1D1,P为底面ABCD内一动点,P到平面AA1D1D的距离与到直线CC1的距离相等,则P点的轨迹是抛物线的一部分.

(16题图)
查看答案和解析>>
科目:高中数学 来源: 题型:
200 km,远地点B距地面350 km.已知地球半径R=6 371km.

(1)求飞船飞行的椭圆轨道的方程;
(2)飞船绕地球飞行了十四圈后,于16日5时59分返回舱与推进舱分离,结束巡天飞行,飞船共巡天飞行了约6×105 km,问飞船巡天飞行平均速度是多少?(结果精确到1km/s)
查看答案和解析>>
科目:高中数学 来源:2013届上海市高二年级期终考试数学 题型:解答题
(本题满分16分)
如图,在四棱锥 中,底面
中,底面 是矩形.已知
是矩形.已知 .
.
(1)证明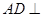 平面
平面 ;
;
(2)求异面直线 与
与 所成的角的大小;
所成的角的大小;
(3)求二面角 的大小.
的大小.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com