
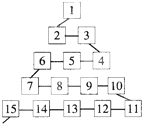
 如图,是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行; 数字2,3出现在第2行; 数字6,5,4(从左至右)出现在第3行,数字7,8,9,10出现在第4行,依此类推,则第63行从左至右的第5个数应是
如图,是网络工作者经常用来解释网络运作的蛇形模型:数字1出现在第1行; 数字2,3出现在第2行; 数字6,5,4(从左至右)出现在第3行,数字7,8,9,10出现在第4行,依此类推,则第63行从左至右的第5个数应是科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
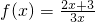 ,数列{an}对n≥2,n∈N总有
,数列{an}对n≥2,n∈N总有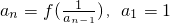 ;
; 的子数列(即{bn}中的每一项都是
的子数列(即{bn}中的每一项都是 的项,且按在
的项,且按在 中的顺序排列)②{bn}为无穷等比数列,它的各项和为
中的顺序排列)②{bn}为无穷等比数列,它的各项和为 .这样的数列是否存在?若存在,求出所有符合条件的数列{bn},写出它的通项公式,并证明你的结论;若不存在,说明理由.
.这样的数列是否存在?若存在,求出所有符合条件的数列{bn},写出它的通项公式,并证明你的结论;若不存在,说明理由.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 第7行 | 84 | 42 | 17 | 53 | 31 | 57 | 24 | 55 | 06 | 88 | 77 | 04 | 74 | 47 | 67 | 21 | 76 | 33 | 50 | 25 | 83 | 92 | 12 | 06 | 76 |
| 第8行 | 63 | 01 | 63 | 78 | 59 | 16 | 95 | 55 | 67 | 19 | 98 | 10 | 50 | 71 | 75 | 12 | 86 | 73 | 58 | 07 | 44 | 39 | 52 | 38 | 79 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
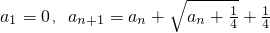 ,令
,令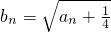 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com