
 中,数列的前n项和
中,数列的前n项和 满足
满足
 ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列 的通项公式并证明,(3) 求
的通项公式并证明,(3) 求
 ,a3=
,a3= ;
; ,证明见解析。
,证明见解析。 =
=
 ,那么对于n令值,那么可知a2=
,那么对于n令值,那么可知a2=

 ,然后运用数学归纳法分两步骤证明即可。
,然后运用数学归纳法分两步骤证明即可。


 成立
成立 假设成立
假设成立 =
= 假设成立
假设成立
 +(
+( )+(
)+( )+…+(
)+…+( )=
)=

 由①②③可证明假设an=
由①②③可证明假设an= 成立
成立
 =
=


科目:高中数学 来源:不详 题型:解答题
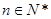 时,令
时,令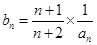 ,
,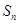 是数列{bn}的前n项和,求证:
是数列{bn}的前n项和,求证: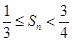
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
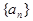 是等和数列,且
是等和数列,且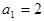 ,公和为5,那么
,公和为5,那么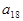 的值为: _ ;这个数列的前n项和
的值为: _ ;这个数列的前n项和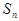 的计算公式为:_ ___.
的计算公式为:_ ___. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com