
如图,![]() 平面
平面![]() ,四边形
,四边形![]() 是正方形,
是正方形,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.

(1)求二面角![]() 的大小;
的大小;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离。
的距离。
略
解法一:(1)∵![]() ⊥平面
⊥平面![]() ,
,
∴ ![]() 是
是![]() 在平面
在平面![]() 上的射影.
上的射影.
由![]() 是正方形知
是正方形知![]() ,
,
∴ ![]() 。
。
∴ ![]() 是二面角
是二面角![]() 的平面角.
的平面角.
∵ ![]() ,∴
,∴ ![]() =45??,
=45??,
即二面角![]() 的大小为45??。………3分
的大小为45??。………3分
(2)如图,建立空![]() 间直角坐标系至
间直角坐标系至![]() ,则
,则
![]() ,
,![]() ,
,![]() ,
,
![]() ,∵
,∵![]() 是
是![]() 的中点,∴
的中点,∴ ![]() ,
,
∴ ![]() ,
,![]() ,
,![]() 。
。
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
平面![]() 的一个法向量为
的一个法向量为![]() 。
。
∴ ![]() ,
,![]() ,即有
,即有![]()
令![]() =1,得x1=-2,y1=-1.
=1,得x1=-2,y1=-1.
∴ ![]() 。
。
同理由![]()
![]() ,
,![]() ,即有
,即有![]()
令z2=1,得x2=0,y2=1,∴ ![]() 。
。
∵ ![]() -2×0+(-1)×1+1×1=0,
-2×0+(-1)×1+1×1=0,
∴ ![]() ,[来源:学*科*网Z*X*X*K]
,[来源:学*科*网Z*X*X*K]
∴ 平面MND⊥平面PCD.……………………………………………………………6分
(3)设![]() 到平面
到平面![]() 的距离为
的距离为![]() 由(2)知平面
由(2)知平面![]() 的法向量
的法向量![]()
∵ ![]() ,
,
∴ |![]() |=4,又 |
|=4,又 |![]() |=
|=![]() ,
,
∴ ![]() =
=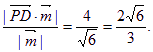
即点P到平面MND的距离为![]() .………………………………………………10分
.………………………………………………10分
解法二:(1)同解法一.
(2)作![]() 的中点
的中点![]() ,连接
,连接![]() ,如图.
,如图.
∵ ![]() 平行且等于
平行且等于![]() ,
,![]() 平行且等于
平行且等于![]() ,
,
∴ ![]() 与
与![]() 平行且相等,于是四边形
平行且相等,于是四边形![]() 是平行四边形,∴
是平行四边形,∴ ![]() //
//![]() 。
。
∵ ![]() ,∴
,∴ ![]() 。∵
。∵ ![]() 面
面![]() ,∴
,∴ ![]() 。又∵
。又∵ ![]() ,
,
∴ ![]() ⊥面
⊥面![]() 。∴
。∴ ![]() 。∴
。∴ ![]() ⊥面
⊥面![]() 。∴
。∴ ![]() ⊥面
⊥面![]() 。
。
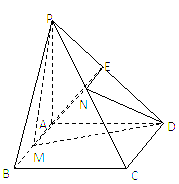 又∵
又∵![]() 面
面![]() ,∴ 平面
,∴ 平面![]() ⊥平面
⊥平面![]() 。……………………6分
。……………………6分
(3)设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
由![]() ,有
,有![]() ,
,
即![]() ,
,![]()
∴ ![]() 。
。
∵ 在![]() 中,
中,![]() .
.
又![]() ,
,![]() ,∴
,∴![]() ,
,
即![]() 到平面
到平面![]() 的距离为
的距离为![]() 。…………………………………………………10分
。…………………………………………………10分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013届度宁夏高二上学期期末考试理科数学试卷 题型:解答题
如图, 平面
平面 ,四边形
,四边形 是正方形,
是正方形, ,点
,点 、
、 、
、 分别为线段
分别为线段 、
、 和
和 的中点. 在线段
的中点. 在线段 上是否存在一点
上是否存在一点 ,使得点
,使得点 到平面
到平面 的距离恰为
的距离恰为 ?若存在,求出线段
?若存在,求出线段 的长;
的长;

若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二下学期第一次阶段考数学理科试卷 题型:解答题
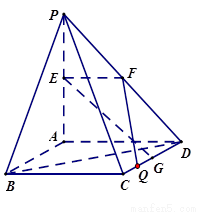
如图, 平面
平面 ,四边形
,四边形 是正方形,
是正方形,  ,点
,点 、
、 、
、 分别为线段
分别为线段 、
、 和
和 的中点.
的中点.
(1)求异面直线 与
与 所成角的余弦值;
所成角的余弦值;
(2)在线段 上是否存在一点
上是否存在一点 ,使得点
,使得点 到平面
到平面 的距离恰为
的距离恰为 ?若存在,求出线段
?若存在,求出线段 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2013届广东省高二第一学期期末考试理科数学 题型:解答题
(本题满分14分)
如图, 平面
平面 ,四边形
,四边形 是矩形,
是矩形, ,
, 与平面
与平面 所成角是
所成角是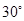 ,点
,点 是
是 的中点,点
的中点,点 在矩形
在矩形 的边
的边 上移动.
上移动.
(1)证明:无论点 在边
在边 的何处,都有
的何处,都有 ;
;
(2)当 等于何值时,二面角
等于何值时,二面角 的大小为
的大小为 .
.

查看答案和解析>>
科目:高中数学 来源:2010年四川省高二下学期期中考试数学卷(文) 题型:解答题
如图, 平面
平面 ,四边形
,四边形 是正方形,
是正方形, ,
, 、
、 分别是
分别是 、
、 的中点.
的中点.

(1)求二面角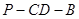 的大小;
的大小;
(2)求证:平面 平面
平面 ;
;
(3)求点 到平面
到平面 的距离。
的距离。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com