
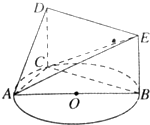
 如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=$\frac{1}{2}$.
如图所示,已知△ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,DC⊥平面ABC,AB=2,tan∠EAB=$\frac{1}{2}$.分析 (I)欲证平面ACD⊥平面ADE,根据面面垂直的判定定理可知在平面ADE内一直线与平面ACD垂直,而根据BC⊥平面ADC,DE∥BC,可得DE⊥平面ADC;
(2II)先利用等体积法表示出三棱锥A-CBE的体积,利用基本不等式求最值,由面ACD⊥平面ADE可知,过点D作DF⊥CE交CE于点F,有FD⊥面ACE,连AF,则∠DAF为直线AD与面ACE所成的角,即可求得直线AD与平面ACE所成角的正弦值.
解答 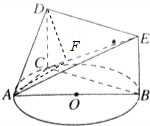 (I)证明:因为四边形DCBE是平行四边形,所以CD∥BE,CB∥DE,因为DC⊥平面ABC,BC?平面ABC,所以DC⊥BC.因为AB是圆O的直径,所以BC⊥AC,又DC∩AC=C,且DC,AC在平面ACD内,所以BC⊥平面ACD,因为DE∥BC,所以DE⊥平面ACD,又DE?平面ADE,所以平面ACD⊥平面ADE.…(6分)
(I)证明:因为四边形DCBE是平行四边形,所以CD∥BE,CB∥DE,因为DC⊥平面ABC,BC?平面ABC,所以DC⊥BC.因为AB是圆O的直径,所以BC⊥AC,又DC∩AC=C,且DC,AC在平面ACD内,所以BC⊥平面ACD,因为DE∥BC,所以DE⊥平面ACD,又DE?平面ADE,所以平面ACD⊥平面ADE.…(6分)
(II)解:由(I)可知BE⊥面ABC,
∴VC-ABE=VE-ABC=$\frac{1}{3}$S△ABC•BE=$\frac{1}{6}•AC•BC•BE$,
∵AB=2,tan∠EAB=$\frac{1}{2}$,∴BE=1,
又AC2+BC2=4,AC•BC≤2,取等号时AC=$\sqrt{2}$,
由面ACD⊥平面ADE可知,过点D作DF⊥CE交CE于点F,有FD⊥面ACE,连AF,则∠DAF为直线AD与面ACE所成的角,∵DF=$\frac{\sqrt{6}}{3}$,AD=$\sqrt{3}$,
∴sin∠DAF=$\frac{\sqrt{2}}{3}$. …(13分)
点评 本题主要考查空间中的线面关系,考查面面垂直的判定及简单组合体体积的计算,考查线面角,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ρcosθ=$\sqrt{3}$ | B. | ρcosθ=-$\sqrt{3}$ | C. | ρsinθ=1 | D. | ρsinθ=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com