
分析 (1)求出函数的导数,问题转化为x2-(a+1)x+a≤0在(1,3)上恒成立,求出a的范围即可;
(2)求出函数的导数,解关于导函数的不等式,求出函数f(x)的最小值,证出结论即可.
解答 解:(1)函数f(x)的定义域为(0,+∞),
$f'(x)=\frac{a}{x}+x-(a+1)=\frac{{{x^2}-(a+1)x+a}}{x}$,
因为函数f(x)在(1,3)上单调增,
故f'(x)≤0即x2-(a+1)x+a≤0在(1,3)上恒成立,
∴a≥x,∴a≥3.
(2)证明:当a=-1时,$f(x)=-lnx+\frac{x^2}{2}$,
$f'(x)=-\frac{1}{x}+x=\frac{(x+1)(x-1)}{x}$,
令f'(x)=0得x=1或x=-1(舍)
当x变化时,f′(x),f(x)的变化情况如下表:
| x | (0,1) | 1 | (1,+∞) |
| f'(x) | - | 0 | + |
| f(x) | 减 | 极小值 | 增 |
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及转化思想,是一道中档题.


科目:高中数学 来源: 题型:解答题
 如图所示,游乐场中摩天轮匀速逆时针旋转,每转一圈需要6min,其中心距离地面40.5m,摩天轮的半径为40m,已知摩天轮上点P的起始位置在最低点处,在时刻t(min)时点P距离地面的高度为f(t)=Asin(wt+φ)+h(A>0,w>0,-π<φ<0,t≥0).
如图所示,游乐场中摩天轮匀速逆时针旋转,每转一圈需要6min,其中心距离地面40.5m,摩天轮的半径为40m,已知摩天轮上点P的起始位置在最低点处,在时刻t(min)时点P距离地面的高度为f(t)=Asin(wt+φ)+h(A>0,w>0,-π<φ<0,t≥0).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
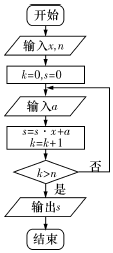 中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=3,n=2,依次输入的a为2,2,5,则输出的s=( )
中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图,执行该程序框图,若输入的x=3,n=2,依次输入的a为2,2,5,则输出的s=( )| A. | 8 | B. | 17 | C. | 29 | D. | 83 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,3) | B. | {1,2} | C. | 0,3) | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com