
【题目】如图,三棱柱ABC﹣A'B'C',AC=2,BC=4,∠ACB=120°,∠ACC'=90°,且平面AB'C⊥平面ABC,二面角A'﹣AC﹣B'为30°,E、F分别为A'C、B'C'的中点.

(1)求证:EF∥平面AB'C;
(2)求B'到平面ABC的距离;
(3)求二面角A﹣BB'﹣C'的余弦值.
【答案】(1)见解析(2)6(3)![]() .
.
【解析】
(1)利用线面平行的判定,求得![]() 后即可得解;
后即可得解;
(2)过![]() 作
作![]() 平面
平面![]() ,转化条件后即可得解;
,转化条件后即可得解;
(3)建立空间坐标系,求出两个面的法向量即可得解.
(1)证明:∵三棱柱![]() 中,四边形
中,四边形![]() 是平行四边形,
是平行四边形,
![]() ,∴
,∴![]() 是
是![]() 的中点,
的中点,
∵![]() 是
是![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(2)过![]() 作
作![]() 平面
平面![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
过点![]() 作
作![]() 的平行线
的平行线![]() ,交
,交![]() 于点
于点![]() ,连结
,连结![]() ,
,
则![]() 是二面角
是二面角![]() 的平面角,
的平面角,
∵![]() ,
,![]() ,
,![]() ,
,![]() 且平面
且平面![]() 平面
平面![]() ,二面角
,二面角![]() 为
为![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() 到平面
到平面![]() 的距离
的距离![]() .
.
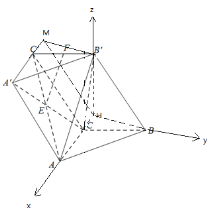
(3)以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则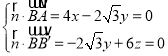 ,取
,取![]() ,得
,得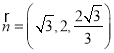 ,
,
设平面![]() 的法向量
的法向量![]() ,
,
则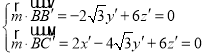 ,取
,取![]() ,得
,得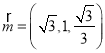 ,
,
设二面角![]() 的平面角为
的平面角为![]() .
.
则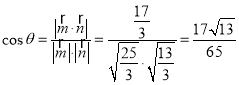 .
.
∴二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知线段AB的端点B的坐标是(4,2),端点A在圆C:(x+2)2+y2=16上运动.
(1)求线段AB的中点的轨迹方程H.
(2)判断(1)中轨迹H与圆C的位置关系.
(3)过点P(3,2)作两条相互垂直的直线MN,EF,分别交(1)中轨迹H于M,N和E,F,求四边形MNFE面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() 、
、![]() ,
,![]() ,点
,点![]() 在椭圆上,且
在椭圆上,且![]() 的周长为
的周长为![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若点![]() 的坐标为
的坐标为![]() ,不过原点
,不过原点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,设线段
两点,设线段![]() 的中点为
的中点为![]() ,点
,点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,且
,且![]() ,
,![]() ,
,![]() 三点共线,求
三点共线,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知椭圆![]() :
: ![]() 的长轴为
的长轴为![]() ,过点
,过点![]() 的直线
的直线![]() 与
与![]() 轴垂直,椭圆
轴垂直,椭圆![]() 上一点与椭圆
上一点与椭圆![]() 的长轴的两个端点构成的三角形的最大面积为2,且椭圆的离心率为
的长轴的两个端点构成的三角形的最大面积为2,且椭圆的离心率为![]() .
.

(1)求椭圆![]() 的标准方程;
的标准方程;
(2) 设![]() 是椭圆
是椭圆![]() 上异于
上异于![]() ,
, ![]() 的任意一点,连接
的任意一点,连接![]() 并延长交直线
并延长交直线![]() 于点
于点![]() ,
, ![]() 点为
点为![]() 的中点,试判断直线
的中点,试判断直线![]() 与椭圆
与椭圆![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
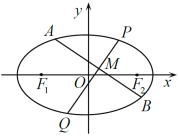
【题目】如图,![]() 、
、![]() 是离心率为
是离心率为![]() 的椭圆
的椭圆![]() :
:![]() 的左、右焦点,过
的左、右焦点,过![]() 作
作![]() 轴的垂线交椭圆
轴的垂线交椭圆![]() 所得弦长为
所得弦长为![]() ,设
,设![]() 、
、![]() 是椭圆
是椭圆![]() 上的两个动点,线段
上的两个动点,线段![]() 的中垂线与椭圆
的中垂线与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点
的中点![]() 的横坐标为1.
的横坐标为1.
(1)求椭圆![]() 的方程;
的方程;
(2)求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】4月23日是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下图是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜”.
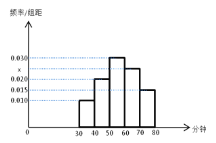
(1)求![]() 的值并估计全校3000名学生中读书谜大概有多少名?(将频率视为概率)
的值并估计全校3000名学生中读书谜大概有多少名?(将频率视为概率)
(2)根据已知条件完成下面![]() 的列联表,并据此判断是否有
的列联表,并据此判断是否有![]() 的把握认为“读书谜”与性别有关?
的把握认为“读书谜”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 40 | ||
女 | 25 | ||
合计 |
附: ,
,![]() .
.
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了推动数学教学方法的改革,学校将高一年级部分生源情况基本相同的学生分成甲乙两个班,每班各40人,甲班按原有模式教学,乙班实施教学方法改革.经过一年的教学实验,将甲乙两个班学生一年来的数学成绩取平均数,两个班学生的平均成绩均在![]() ,按照区间
,按照区间![]() ,
,![]() ,
,![]() 进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
进行分组,绘制成如下频率分布直方图,规定不低于80分(百分制)为优秀.
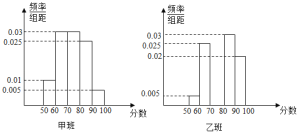
(1)完成表格,并判断是否有90%以上的把握认为“数学成绩优秀与教学改革有关”;
甲班 | 乙班 | 总计 | |
大于等于80分的人数 | |||
小于80分的人数 | |||
总计 |
(2)从乙班![]() 分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自
分数段中,按分层抽样随机抽取7名学生座谈,从中选三位同学发言,记来自![]() 发言的人数为随机变量
发言的人数为随机变量![]() ,求
,求![]() 的分布列和期望.附:
的分布列和期望.附: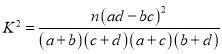 ,
,
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com