
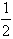 AD。
AD。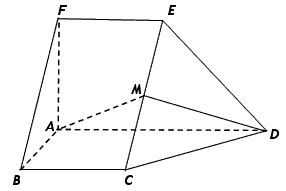
| 解:(1)由题设知,BF∥CE, 所以∠CED(或其补角)为异面直线BF与DE所成的角, 设P为AD的中点,连结EP、PC, 因为FE 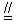 AP, AP,所以FA 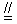 EP, EP,同理AB 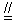 PC, PC,又FA⊥平面ABCD, 所以EP⊥平面ABCD, 而PC、AD都在平面ABCD 内, 故EP⊥PC,EP⊥AD, 由AB⊥AD,可得PC⊥AD 设FA=a,则EP=PC=PD=a, 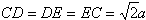 故∠CED=60°, 所以异面直线BF与DE所成的角的大小为60°; (2)因为DC=DE且M为CE的中点, 所以DM⊥CE.连结MP,则MP⊥CE, 又MP∩DM =M, 故CE⊥平面AMD, 而CE  平面CDE, 平面CDE,所以平面AMD⊥平面CDE; (3)设Q为CD的中点,连结PQ、EQ, 因为CE=DE, 所以EQ⊥CD, 因为PC=PD, 所以PQ⊥CD, 故∠EQP为二面角A-CD-E的平面角, 由(1)可得,EP⊥PQ, 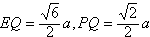 于是在Rt△EPQ中, 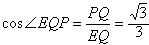 所以二面角A-CD-E的余弦值为 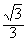 。 。 |
 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
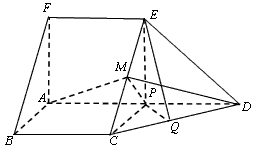
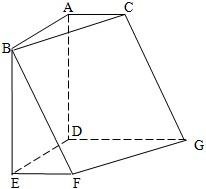 如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.
如图,在六面体ABCDEFG中,平面ABC∥平面DEFG,AD⊥平面DEFG,AB⊥AC,ED⊥DG,EF∥DG.且AB=AD=DE=DG=2,AC=EF=1.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=
如图,在五面体ABCDE中,平面BCD⊥平面ABC,DC=DB=| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2012年辽宁省鞍山一中高考数学五模试卷(理科)(解析版) 题型:解答题
 ,AC=BC=2ED=2,AC⊥BC,且ED∥AC
,AC=BC=2ED=2,AC⊥BC,且ED∥AC  ,求二面角F-AE-B的余弦值.
,求二面角F-AE-B的余弦值.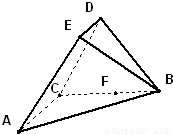
查看答案和解析>>
科目:高中数学 来源:2012年高考数学预测试卷2(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com