
【题目】某高校学生社团为了解“大数据时代”下大学生就业情况的满意度,对20名学生进行问卷计分调查(满分100分),得到如图所示的茎叶图:
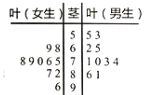
(1)计算男生打分的平均分,观察茎叶图,评价男女生打分的分散程度;
(2)从打分在80分以上的同学随机抽3人,求被抽到的女生人数![]() 的分布列和数学期望.
的分布列和数学期望.
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|loga|x﹣1||(a>0,a≠1),若x1<x2<x3<x4 , 且f(x1)=f(x2)=f(x3)=f(x4),则 ![]() +
+ ![]() +
+ ![]() +
+ ![]() = .
= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥中,PA⊥平面ABCD,底面ABCD是边长为a的菱形,∠BAD=120°,PA=b. 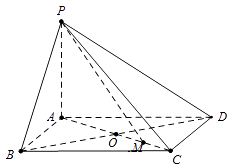
(1)求证:平面PBD⊥平面PAC;
(2)设AC与BD交于点O,M为OC中点,若二面角O﹣PM﹣D的正切值为2 ![]() ,求a:b的值.
,求a:b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]()
(1)计算f(1)+f(0)的值;
(2)计算f(x)+f(1﹣x)的值;
(3)若关于x的不等式:f[23x﹣2﹣x+m(2x﹣2﹣x)+ ![]() ]<
]< ![]() 在区间[1,2]上有解,求实数m的取值范围.
在区间[1,2]上有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=x+ ![]() 有如下性质:如果常数t>0,那么该函数在
有如下性质:如果常数t>0,那么该函数在 ![]() 上是减函数,在
上是减函数,在 ![]() 上是增函数.
上是增函数.
(1)已知f(x)= ![]() ,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
,x∈[﹣1,1],利用上述性质,求函数f(x)的单调区间和值域;
(2)对于(1)中的函数f(x)和函数g(x)=﹣x﹣2a,若对任意x1∈[﹣1,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列三个命题
①若“p或q”为假命题,则p,q均为真命题;
②命题“若x≥2且y≥3,则x+y≥5”的逆否命题为假命题;
③在△ABC中,“A>45°”是“sinA> ![]() ”的充要条件,
”的充要条件,
其中正确的命题个数是( )
A.3
B.2
C.1
D.0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com