
| 月份 | 1 | 2 | 3 | 4 | 5 | 6 |
| 销售量x(万件) | 10 | 11 | 13 | 12 | 8 | 6 |
| 利润y(万元) | 22 | 25 | 29 | 26 | 16 | 12 |
分析 (1)求出$\overline{x}$,$\overline{y}$,由公式,得$\widehat{b}$的值,从而求出$\widehat{a}$的值,从而得到y关于x的线性回归方程,
(2)由(1)能求出该小组所得线性回归方程是理想的.
解答 解:(1)∵$\overline{x}$=11,$\overline{y}$=24,
∴$\widehat{b}$=$\frac{18}{7}$,
故$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$=-$\frac{30}{7}$,
故y关于x的方程是:$\widehat{y}$=$\frac{18}{7}$x-$\frac{30}{7}$;
(2)∵x=10时,$\widehat{y}$=$\frac{150}{7}$,
误差是|$\frac{150}{7}$-22|=$\frac{4}{7}$<1,
x=6时,$\widehat{y}$=$\frac{78}{7}$,误差是|$\frac{78}{7}$-12|=$\frac{6}{7}$<1,
故该小组所得线性回归方程是理想的.
点评 本题考查了求回归方程问题,考查残差的计算,是一道基础题.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源: 题型:选择题

| A. | f(x)的图象关于直线x=-$\frac{2π}{3}$对称 | |
| B. | 函数f(x)在[-$\frac{π}{3}$,0]上单调递增 | |
| C. | f(x)的图象关于点(-$\frac{5π}{12}$,0)对称 | |
| D. | 将函数y=2sin(2x-$\frac{π}{6}$)的图象向左平移$\frac{π}{6}$个单位得到f(x)的图象 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
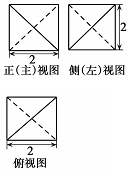
| A. | 2$\sqrt{3}$ | B. | $\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com