练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．下面有命题：
    ①y=|sinx-$\frac{1}{2}$|的周期是π；
    ②y=sinx+sin|x|的值域是[0，2]；
    ③方程cosx=lgx有三解；
    ④ω为正实数，y=2sinωx在$[-\frac{π}{3}，\frac{2π}{3}]$上递增，那么ω的取值范围是$（0，\frac{3}{4}]$；  
    ⑤在y=3sin（2x+$\frac{π}{4}$）中，若f（x1）=f（x2）=0，则x1-x2必为π的整数倍；
    ⑥若A、B是锐角△ABC的两个内角，则点P（cosB-sinA，sinB-cosA在第二象限；
    ⑦在△ABC中，若$\overrightarrow{AB}•\overrightarrow{BC}＞0$，则△ABC钝角三角形．其中真命题个数为（　　）
    A．2B．3C．4D．5

    分析 ①，∵y=|sin（ωx-$\frac{1}{2}$|的周期是$\frac{π}{ω}$，；
    ②，当x≥0时，y=sinx+sin|x|=2sinx值域不是[0，2]，；
    ③，∵lg2π＜1，lg4π＞1，方程cosx=lgx有三解，正确；
    ④，ω为正实数，y=2sinωx在$[-\frac{π}{3}，\frac{2π}{3}]$上递增，由条件利用正弦函数的单调性可得ω•$\frac{2π}{3}≤\frac{π}{2}$≤，由此求得正数ω的范围是$（0，\frac{3}{4}]$，；  
    ⑤，函数的周期T=π，函数值等于0的x之差的最小值为$\frac{T}{2}$，所以x1-x2必是$\frac{π}{2}$的整数倍；
    ⑥，若A、B是锐角△ABC的两个内角，$\frac{π}{2}＞\\;B＞\frac{π}{2}-A$B＞$\frac{π}{2}$-A，则 cosB-sinA＜0，sinB-cosA＞0，；

    解答 解：对于①，∵y=|sin（ωx-$\frac{1}{2}$|的周期是$\frac{π}{ω}$，故正确；
    对于②，当x≥0时，y=sinx+sin|x|=2sinx值域不是[0，2]，故错；
    对于③，∵lg2π＜1，lg4π＞1，方程cosx=lgx有三解，正确；
    对于④，ω为正实数，y=2sinωx在$[-\frac{π}{3}，\frac{2π}{3}]$上递增，由条件利用正弦函数的单调性可得ω•$\frac{2π}{3}≤\frac{π}{2}$≤，由此求得正数ω的范围是$（0，\frac{3}{4}]$，故正确；  
    对于⑤，函数的周期T=π，函数值等于0的x之差的最小值为$\frac{T}{2}$，所以x1-x2必是$\frac{π}{2}$的整数倍．故错；
    对于⑥，若A、B是锐角△ABC的两个内角，$\frac{π}{2}＞\\;B＞\frac{π}{2}-A$B＞$\frac{π}{2}$-A，则 cosB-sinA＜0，sinB-cosA＞0，故正确；
    故选：C．

    点评 本题考查了命题的真假，涉及到三角函数的知识，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=$\frac{x}{x+2}$-ax2，其中a∈R．
    （1）若a=1时，求函数f（x）的零点；
    （2）当a＞0时，求证：函数f（x）在（0，+∞）内有且仅有一个零点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．在数列{an}中，a1=-2，an+1=an-2n，则a2017的值为（　　）
    A．22016B．22018C．-22017D．22017

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．某百货公司1～6月份的销售量x与利润y的统计数据如表：
    月份123456
    销售量x（万件）1011131286
    利润y（万元）222529261612
    （1）根据2～5月份的统计数据，求出y关于x的回归直线方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$；
    （2）若由回归直线方程得到的估计数据与剩下的检验数据的误差均不超过2万元，则认为得到的回归直线方程是理想的，试问所得回归直线方程是否理想？
    （参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$）=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-b$\overline{x}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．$cos（-\frac{19π}{6}）$的值为．（　　）
    A．$\frac{1}{2}$B．$-\frac{1}{2}$C．$\frac{{\sqrt{3}}}{2}$D．$-\frac{{\sqrt{3}}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．函数f（x）=aln（x2+1）+bx，g（x）=bx2+2ax+b，（a＞0，b＞0）．已知方程g（x）=0有两个不同的非零实根x1，x2．
    （1）求证：x1+x2＜-2；
    （2）若实数λ满足等式f（x1）+f（x2）+3a-λb=0，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    13．已知函数f（x）（x∈R）满足f（x+π）=f（x）+cosx，当0≤x＜π时，f（x）=-1，则f（$\frac{2017π}{3}$）=（　　）
    A．$\frac{1}{2}$B．$-\frac{1}{2}$C．$\frac{{\sqrt{3}}}{2}$D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知等比数列{an}中，an+1=36，an+3=m，an+5=4，则圆锥曲线$\frac{{x}^{2}}{m}$+$\frac{{y}^{2}}{3}$=1的离心率为（　　）
    A．$\sqrt{5}$B．$\frac{\sqrt{3}}{2}$C．$\sqrt{5}$或$\frac{\sqrt{3}}{2}$D．$\frac{\sqrt{5}}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．阅读如图的程序框图，运行相应的程序，则输出的值为（　　）
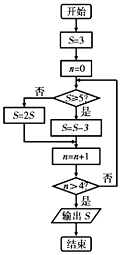
    A．3B．4C．6D．7

    查看答案和解析>>

    同步练习册答案