练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设关于x的二次方程中，其中a，b，c是钝角三角形的三边，且b最大．

    (1)证明这个方程有相异的正实根．

    (2)当a=c，且两根之差的绝对值等于时，求B．

    答案：略
    解析：

    (1)证明：∵b最大，∴角B为钝角．∴cosB＜0．

    ，

    ∵，∴Δ＞0．

    ∴方程有两相异实根．又两根之和为，两根之积为均为正数，

    ∴方程有两个相异正实根

    (2)解：设方程的两根为a ，β．

    当a=c时

    又由时有，

    ∴，∴．

    ∴B=120°．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设关于x的一元二次方程x2+2ax+b2=0．
    （1）若a是从0，1，2，3四个数中任取的一个数，b是从0，1，2三个数中任取的一个数，求上述方程有实根的概率．
    （2）若a是从区间[0，3]任取的一个数，b是从区间[0，2]任取的一个数，求上述方程有实根的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设关于x的一元二次方程x2-mx+
    14
    n2=0    ；
    （1）若m是从0，1，2，3四个数中任取的一个数，n是从0，1，2三个数中任取的一个数，求上述方程有实根的概率；
    （2）若m是从区间[0，3]内任取的一个数，n是从区间[0，2]内任取的一个数，求上述方程有实根的概率．

    查看答案和解析>>

    科目：高中数学 来源：高中教材（试验本）助学丛书·数学高一年级·第二册 题型：044

    设关于x的二次方程中，其中a，b，c是钝角三角形的三边，b边最大．

    (1)证明这个方程有相异的正实根；

    (2)当a=c时，求两根之差的绝对值的变化范围；

    (3)当a=c，且两根之差的绝对值等于时，求B

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：044

    设关于x的二次方程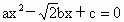中，其中a，b，c是钝角三角形的三边，且b最大．

    (1)证明这个方程有相异的正实根．

    (2)当a=c，且两根之差的绝对值等于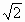时，求B．

    查看答案和解析>>

    同步练习册答案