练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知＝(1，2sinx)＝(cos2x，－cosx)设函数f(x)＝·．

    (1)若x，求f(x)的最大值、最小值并求出对应的x值；

    (2)求f(x)在区间[－π，0]的递减区间．

    答案：
    解析：

    　　解：(1)f(x)＝cosx－2sinx·cosx＝cosx－sin2x＝2cos(2x＋)．

    　　

    　　(2)，

    　　


    提示：

    　　分析：(1)利用三角公式化简表达式，求最值时注意定义域．

    　　(2)简单的复合函数的单调区间的求法．

    　　说明：近两年江苏试题没有向量与三角的解答题，而其它省市多以这样的题目作为解答题的第1题，而三角公式、函数的图象及性质也是命题重点，因这样的目的出此题．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2007年综合模拟数学卷三 题型：013

    已知＝(2cosθ，2sinθ)．θ∈(，π)，＝(0，－1)．则与夹角是

    [　　]

    A．－θ

    B．＋θ

    C．θ－

    D．θ

    查看答案和解析>>

    科目：高中数学 来源：海南省洋浦中学2010-2011学年高一上学期期末考试数学试题 题型：013

    已知a＝(cos2α，sinα)，b＝(1，2sinα－1)，α∈(，π)，若a·b＝，则tan(α＋)的值是

    [　　]
    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：高中数学 来源：2011届高考数学第一轮复习测试题9 题型：044

    (文)已知a＝(cos2α，sinα)，b＝(1，2sinα－1)，α∈(，π)，a·b＝，求cos(α＋)的值．

    查看答案和解析>>

    科目：高中数学 来源：四川省双流中学2012届高三下学期第一次月考数学试题 题型：044

    已知＝(sin(ωx－)，1)，＝(2sin(ωx＋)，1)，函数f(x)＝·－1的最小正周期为π(其中ω为正常数，x∈R)．

    (Ⅰ)求ω的值和函数f(x)的递增区间；

    (Ⅱ)在△ABC中，若A＜B，且f(A)＝f(B)＝，求．

    查看答案和解析>>

    科目：高中数学 来源：2013-2014学年河南省原名校高三上学期期联考文科数学试卷（解析版） 题型：解答题

    已知函数f（x）＝2sin（ωx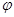＋）（ω＞0，0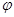＜＜π）的图象如图所示．

    （1）求函数f（x）的解析式：

    （2）已知＝，且a∈（0，），求f（a）的值．

     

    查看答案和解析>>

    同步练习册答案