
【题目】已知函数![]() ,
,![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(1)当![]() 时,证明:
时,证明:![]() ,
,![]() ;
;
(2)若函数![]() 在
在![]() 上存在两个极值点,求实数
上存在两个极值点,求实数![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)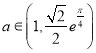
【解析】
(1)先求导,再利用导数研究函数的单调性从而得证;
(2)先求导数![]() ,再讨论当
,再讨论当![]() 时,当
时,当![]() 时,函数的单调性及极值情况,再求解即可.
时,函数的单调性及极值情况,再求解即可.
(1)当![]() 时,
时,![]() ,则
,则![]() ,
,
当![]() 时,
时,![]() ,则
,则![]() ,又因为
,又因为![]() ,
,
所以当![]() 时,
时,![]() ,仅
,仅![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上是单调递减,所以
上是单调递减,所以![]() ,即
,即![]() .
.
(2)![]() ,因为
,因为![]() ,所以
,所以![]() ,
,![]() ,
,
①当![]() 时,
时,![]() 恒成立,所以
恒成立,所以![]() 在
在![]() 上单调递增,没有极值点.
上单调递增,没有极值点.
②当![]() 时,
时,![]() ,令
,令![]() ,
,
则![]() 在
在![]() 上单调递减,因为
上单调递减,因为![]() ,
,![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ,
,![]() ,
,
所以![]() 在
在![]() 上单调递增,
上单调递增,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,即
,即![]() ,所以
,所以![]() 单调递减,无极值点;
单调递减,无极值点;
当![]() ,即
,即![]() 时,存在
时,存在![]() ,使
,使![]() ,
,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减,
单调递减,![]() 在
在![]() 处取极大值,
处取极大值,
因为![]() ,所以
,所以![]() ,又因为
,又因为![]() ,
,![]() ,
,
若![]() 存在两个极值点,即
存在两个极值点,即![]() 存在两个变号零点,则
存在两个变号零点,则![]() 得
得![]() ,
,![]() 得
得![]() ,得
,得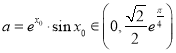 ,
,
此时存在![]() ,
,![]() 使得
使得![]() ,
,![]() ,
,
当![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,即
,即![]() 在
在![]() 处取得极小值,在
处取得极小值,在![]() 处取得极大值,
处取得极大值,![]() ,
,![]() 为
为![]() 的两个极值点,则此时
的两个极值点,则此时![]() .
.
综上可知若函数![]() 在
在![]() 上存在两个极值点,则实数
上存在两个极值点,则实数![]() 的取值范围为:
的取值范围为: .
.


 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案科目:高中数学 来源: 题型:
【题目】已知甲盒内有大小相同的2个红球和3个黑球,乙盒内有大小相同的3个红球和3个黑球,现从甲,乙两个盒内各取2个球.
(1)求取出的4个球中恰有1个红球的概率;
(2)设ξ为取出的4个球中红球的个数,求ξ的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
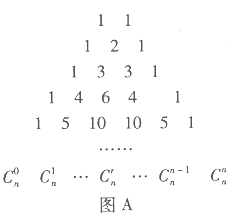
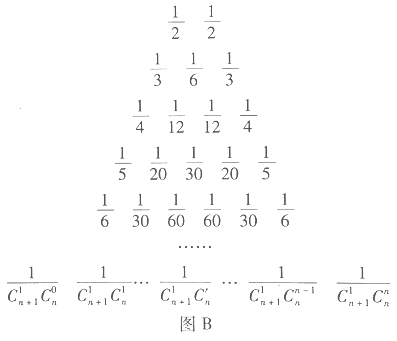
【题目】在我国南宋数学家杨辉所著的《详解九章算法》(1261年)一书中,用如图![]() 所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”
所示的三角形,解释二项和的乘方规律.在欧洲直到1623年以后,法国数学家布莱士帕斯卡的著作(1655年)介绍了这个三角形,近年来,国外也逐渐承认这项成果属于中国,所以有些书上称这是“中国三角形”![]() ,如图
,如图![]() .17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图
.17世纪德国数学家莱布尼茨发现了“莱布尼茨三角形”,如图![]() .在杨辉三角中,相邻两行满足关系式:
.在杨辉三角中,相邻两行满足关系式:![]() ,其 中
,其 中![]() 是行数,
是行数,![]() .请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是__________.
.请类比上式,在莱布尼茨三角形中相邻两行满足的关系式是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,
,![]() 是它的上顶点,点
是它的上顶点,点![]() 各不相同且均在椭圆上.
各不相同且均在椭圆上.
(1)若![]() 恰为椭圆长轴的两个端点,求
恰为椭圆长轴的两个端点,求![]() 的面积;
的面积;
(2)若![]() ,求证:直线
,求证:直线![]() 过一定点;
过一定点;
(3)若![]() ,
,![]() 的外接圆半径为
的外接圆半径为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度得到
个单位长度得到![]() 的图象,若
的图象,若![]() 的对称中心为坐标原点,则关于函数
的对称中心为坐标原点,则关于函数![]() 有下述四个结论:
有下述四个结论:
①![]() 的最小正周期为
的最小正周期为![]() ②若
②若![]() 的最大值为2,则
的最大值为2,则![]()
③![]() 在
在![]() 有两个零点 ④
有两个零点 ④![]() 在区间
在区间![]() 上单调
上单调
其中所有正确结论的标号是( )
A.①③④B.①②④C.②④D.①③
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 常数
常数![]() )满足
)满足![]() .
.
(1)求出![]() 的值,并就常数
的值,并就常数![]() 的不同取值讨论函数
的不同取值讨论函数![]() 奇偶性;
奇偶性;
(2)若![]() 在区间
在区间![]() 上单调递减,求
上单调递减,求![]() 的最小值;
的最小值;
(3)在(2)的条件下,当![]() 取最小值时,证明:
取最小值时,证明:![]() 恰有一个零点
恰有一个零点![]() 且存在递增的正整数数列
且存在递增的正整数数列![]() ,使得
,使得![]() 成立.
成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以原点
中,以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.若曲线
轴正半轴为极轴建立极坐标系.若曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 点的极坐标为
点的极坐标为![]() ,在平面直角坐标系中,直线
,在平面直角坐标系中,直线![]() 经过点
经过点![]() ,且倾斜角为
,且倾斜角为![]() .
.
(1)写出曲线![]() 的直角坐标方程以及点
的直角坐标方程以及点![]() 的直角坐标;
的直角坐标;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 参数方程为
参数方程为![]() 为参数),将曲线
为参数),将曲线![]() 上所有点的横坐标变为原来的
上所有点的横坐标变为原来的![]() ,纵坐标变为原来的
,纵坐标变为原来的![]() ,得到曲线
,得到曲线![]() .
.
(1)求曲线![]() 的普通方程;
的普通方程;
(2)过点![]() 且倾斜角为
且倾斜角为![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 取得最小值时
取得最小值时![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了了解运动健身减肥的效果,某健身房调查了20名肥胖者,健身之前他们的体重情况如三维饼图(1)所示,经过四个月的健身后,他们的体重情况,如三维饼图(2)所示.对比健身前后,关于这20名肥胖者,下面结论不正确的是( )
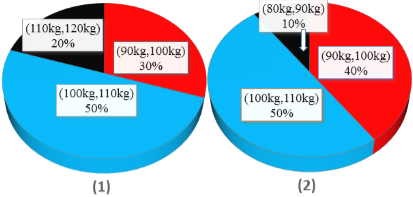
A.他们健身后,体重在区间![]() 内的人增加了2个
内的人增加了2个
B.他们健身后,体重在区间![]() 内的人数没有改变
内的人数没有改变
C.他们健身后,20人的平均体重大约减少了8 kg
D.他们健身后,原来体重在区间![]() 内的肥胖者体重都有减少
内的肥胖者体重都有减少
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com