证明:由题设f(x)对任意实数x
1、x
2都满足f(x
1)+f(x
2)=2f(

)(
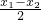
),且f(

)=0,f(x)不恒等于0,
(1)令x
1=x
2=0,得f(0)+f(0)=2f(0)×f(0),即2f(0)×[f(0)-1]=0,故f(0)=0或f(0)=1,
若f(0)=0,则f(x)+f(x)=2f(x)f(0)=0,故对任意的x有f(x)═0恒成立,这与f(x)不恒等于0矛盾,
故f(0)=1;
(2)f(x+π)+f(x)=2f(x+

)f(

)=0,∴f(x+π)=-f(x);
(3)由(2)的结论知f(x+2π)-f(x)=f(x+2π)+f(x+π)=2f(x+

)×f(

)=0,∴f(x+2π)=f(x)
(4)∵f(x)-f(-x)=f(x)+f(-x+π)=2f(x-

)f(

)=0,∴f(x)=f(-x);
(5)∵f(2x)+1=f(2x)+f(0)=2f
2(x),∴f(2x)=2f
2(x)-1
分析:观察题设条件可以看出,本题的证明可以借助同性质的余弦函数的性质来证明.本题中各个小题之间有一定的关系,后一个的证明要充分利用前一个的结论.
(1)赋值求值,令x
1=x
2=0,得f(0)的方程,解方程求值,解出的两个解中有一个需要排除,本小题的证明稍嫌繁琐.
(2)利用(1)结论与题设中所给的恒等关系证明f(x+π)=-f(x)的等价形式f(x+π)+f(x)=0;
(3)利用(2)的结论证明其等价方程f(x+2π)-f(x)=0;
(4)利用(2)的结论证明其等价方程f(x)-f(-x)=0;
(5)利用(1)的结论凑成题设中的恒等式的形式进行恒等变形证其等价形式f(2x)+1=2f
2(x).
点评:本题的考点是抽象函数的证明,在求解此类题目时,应发挥自己的想象力,看它的性质与自己熟悉的那一个函数比较类似,参考相关的函数的性质来证明这个抽象函数是破题的一个好办法.

 )(
)(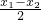 ),且f(
),且f( )=0,f(x)不恒等于0,求证:
)=0,f(x)不恒等于0,求证: )(
)(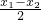 ),且f(
),且f( )=0,f(x)不恒等于0,
)=0,f(x)不恒等于0, )f(
)f( )=0,∴f(x+π)=-f(x);
)=0,∴f(x+π)=-f(x); )×f(
)×f( )=0,∴f(x+2π)=f(x)
)=0,∴f(x+2π)=f(x) )f(
)f( )=0,∴f(x)=f(-x);
)=0,∴f(x)=f(-x);
