练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:

    (1)CD=BC.

    (2)△BCD∽△GBD.

    【证明】(1)因为D,E分别为AB,AC的中点,所以DE∥BC.又已知CF∥AB,故四边形BCFD是平行四边形,所以CF=BD=AD.而CF∥AD,连接AF,所以四边形ADCF是平行四边形,故CD=AF.因为CF∥AB,所以BC=AF,故CD=BC.

    (2)∵D,E分别为AB,AC的中点,　

    ∴FG∥BC,∴GB=CF.

    由(1)知BD=CF,则GB=BD,∴∠BGD=∠BDG,

    又由(1)知BC=CD,∴∠CBD=∠CDB,

    ∵∠BDG=∠CBD,∴∠CBD=∠CDB=∠BDG=∠BGD,∴△BCD∽△GBD.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2013-2014学年人教版高考数学文科二轮专题复习提分训练12练习卷（解析版） 题型：解答题

    如图所示,D,E分别为△ABC的边AB,AC上的点,且不与△ABC的顶点重合.已知AE的长为m,AC的长为n,AD,AB的长是关于x的方程x2-14x+mn=0的两个根.

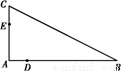
    (1)证明:C,B,D,E四点共圆;

    (2)若∠A=90°,且m=4,n=6,求C,B,D,E所在圆的半径.

     

    查看答案和解析>>

    科目：高中数学 来源：2012年全国普通高等学校招生统一考试文科数学（北京卷解析版） 题型：解答题

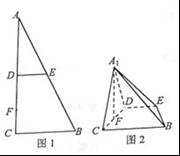
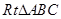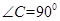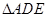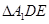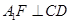    如图1，在中，，D,E分别为AC，AB的中点，点F为线段CD上的一点，将沿DE折起到的位置，使，如图2.

    （Ⅰ）求证：DE∥平面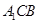

    （Ⅱ）求证：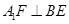

    （Ⅲ）线段上是否存在点Q，使？说明理由。

    【解析】（1）∵DE∥BC，由线面平行的判定定理得出

    （2）可以先证，得出，∵∴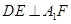

    ∴

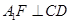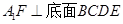
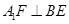
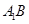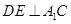    (3)Q为的中点，由上问，易知,取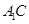中点P，连接DP和QP，不难证出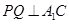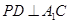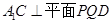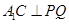，∴∴,又∵∴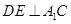

     

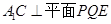
    查看答案和解析>>

    科目：高中数学 来源： 题型：

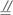
    如图2-2-9,在直三棱柱ABC—A1B1C1中,AB=BC,D,E分别为BB1、AC1的中点.

    图2-2-9

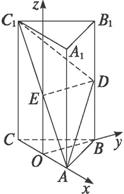
    (1)证明ED为异面直线BB1与AC1的公垂线;

    (2)设AA1=AC=AB,求二面角A1-AD-C1的大小.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在直三棱柱ABC—A1B1C1中,AB=BC,D,E分别为BB1,AC1的中点.

    (1)证明:ED为异面直线BB1与AC1的公垂线;

    (2)设AA1=AC=AB,求二面角A1—AD—C1的大小.

    查看答案和解析>>

    同步练习册答案