练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    若从集合{x|x2-9x≤10，x∈N}中任取三个不同的元素，则所取的三个元素可以构成等差数列的概率为________（填具体数值）．


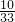
    分析：根据题意求出集合内所有的整数，得到所有的取法，再分类即根据公差的不同求出所取的三个元素可以构成等差数列的取法，进而得到答案．
    解答：{x|x2-9x≤10，x∈N}={x|-1≤x≤10，x∈N}={0，1，2，3，4，5，6，7，8，9，10}
    从集合中任取3个不同的元素，所有的取法有C113=165，
    则所取的三个元素可以构成等差数列的取法有50，
    所以则所取的三个元素可以构成等差数列的概率为．
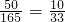
    故答案为：．
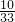
    点评：解决此类问题的关键是熟悉利用列举法计算基本事件数以及事件发生概率的方法（做到不重不漏），结合二次不等式的解法与等差数列的定义解决问题即可．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    若从集合{x|x2-9x≤10，x∈N}中任取三个不同的元素，则所取的三个元素可以构成等差数列的概率为
     
    （填具体数值）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知集合A=B=R+，若f：x→x2是从集合A到B的一个映射，则与B中元素4对应的A中的元素为
    2
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•成都模拟）已知集合A={-1，0，1，2，3，2
    		2
    +1}，集合B={1，2，3，4，5，9}，映射f：A→B的对应法则为f：x→y=x2-2x+2，设集合M={m∈B|m在集合A中存在原象}，集合N={n∈B|n在集合A中不存在原象}，若从集合M、N中各取一个元素组成没有重复数字的两位数的个数（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若从集合{x|x2-9x≤10，x∈N}中任取三个不同的元素，则所取的三个元素可以构成等差数列的概率为______（填具体数值）．

    查看答案和解析>>

    同步练习册答案