Question

在空间直角坐标系中，已知O (0,0,0) ，A(2,－1,3)，B(2,1,1).

(1)求|AB|的长度；

(2)写出A、B两点经此程序框图执行运算后的对应点A₀，B₀的坐标，并求出在方向上的投影.

 

Answer 1

【答案】

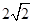（1）；（2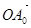）=(2,－1,3)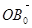，=(2,1,3)；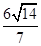

【解析】

试题分析：（1）有空间两点间的距离可得AB两点的距离.本小题关键是考查空间中两点的距离公式，本公式类似平面中两点的距离公式.

（2）由程序框图可知对空间坐标中的z要求符合一个不等式.通过循环结构即可求得符合要求的z的值.根据向量在另一向量的投影即为该向量的模长与这两向量夹角的余弦值的乘积.本小题通过向量知识与立几知识的交汇，难度不大.有新意.

试题解析：在空间直角坐标系中，已知O (0,0,0) ，A(2,－1,3)，B(2,1,1).

(1) 

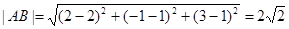
(2)∵A(2,－1,3)满足 2²+(－1)²≤3²

∴输出A₀(2,－1,3)

∵B(2,1,1)不满足2²+1²≤1²

∴z=z+1=2

∵(2,1,2)不满足2²+1²≤2²

∴z=z+1=3

∵(2,1,3)满足2²+1²≤3²

∴输出B₀(2,1,3)

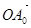∴=(2,－1,3)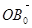，=(2,1,3)

∴

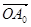∴在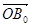方向上的投影等于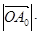

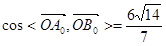
考点：1.空间中两点的距离.2.程序框图.3.空间中的直线关系.