练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    设函数f(x)＝x|x－a|＋b，求证：f(x)为奇函数的充要条件是a2＋b2＝0.

    证明　充分性：∵a2＋b2＝0，∴a＝b＝0，∴f(x)＝x|x|.

    ∵f(－x)＝－x|－x|＝－x|x|，－f(x)＝－x|x|，

    ∴f(－x)＝－f(x)，∴f(x)为奇函数．

    必要性：若f(x)为奇函数，则对一切x∈R，f(－x)＝－f(x)恒成立．

    即－x|－x－a|＋b＝－x|x－a|－b恒成立．

    令x＝0，则b＝－b，∴b＝0，令x＝a，则2a|a|＝0，∴a＝0.

    即a2＋b2＝0.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2002年全国各省市高考模拟试题汇编 题型：044

    设函数f(x)＝(x－1)(a＞0，且a≠1)，当点P(x，y)是函数y＝f(x)图象上的点时，点Q(3x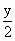，)是函数y＝g(x)图象上的点．

    　　

    (Ⅰ)写出函数y＝g(x)的解析式；

    (Ⅱ)求不等式g(x)≤f(x)的解集．

    查看答案和解析>>

    科目：高中数学 来源：广州市2008届高中教材变式题2：二次函数 题型：022

    设函数f(x)＝x|x|＋bx＋c，给出下列4个命题：

    ①当c＝0时，y＝f(x)是奇函数；

    ②当b＝0，c＞0时，方程f(x)＝0只有一个实根；

    ③y＝f(x)的图象关于点(0，c)对称；

    ④方程f(x)＝0至多有两个实根．

    上述命题中正确的序号为________．

    查看答案和解析>>

    科目：高中数学 来源：天津市耀华中学2012届高三寒假验收考试数学理科试题 题型：013

    设函数f(x)＝x|x|＋bx＋c，则下列命题中正确命题的序号有

    ①当b＞0时，函数f(x)在R上是单调增函数；

    ②当b＜0时，函数f(x)在R上有最小值；

    ③函数f(x)的图象关于(0，c)对称；

    ④方程f(x)＝0可能有三个实数根．

    [　　]

    A．①③

    B．①④

    C．①②④

    D．①③④

    查看答案和解析>>

    科目：高中数学 来源：广东省云浮罗定中学2012届高三11月月考数学理科试题 题型：044

    已知二次函数y＝g(x)的图象经过点O(0，0)、A(m，0)与点P(m＋1，m＋1)，设函数f(x)＝(x－n)g(x)在x＝a和x＝b处取到极值，其中m＞n＞0，b＜a．

    (1)求g(x)的二次项系数k的值；

    (2)比较a，b，m，n的大小(要求按从小到大排列)；

    (3)若m＋n≤2，且过原点存在两条互相垂直的直线与曲线y＝f(x)均相切，求y＝f(x)．

    查看答案和解析>>

    科目：高中数学 来源：2012-2013学年宁夏高三第五次月考理科数学试卷（解析版） 题型：填空题

    设函数f(x)＝，D是由x轴和曲线y＝f(x)及该曲线在点(1,0)处的切线所围成的封闭区域，则z＝x－2y在D上的最大值为________．

     

    查看答案和解析>>

    同步练习册答案