
【题目】已知![]() ,设
,设![]() 成立;
成立; ![]() 成立. 如果“
成立. 如果“![]() ”为真,“
”为真,“![]() ”为假,求实数
”为假,求实数![]() 的取值范围.
的取值范围.
【答案】![]()
【解析】试题分析:若命题p为真,通过分离参变量求出函数![]() ,在
,在![]() 时的最小值,可得m的取值范围;若命题q为真,则
时的最小值,可得m的取值范围;若命题q为真,则![]() 在
在![]() 有解,构造函数
有解,构造函数![]() ,求出函数的最大值,可得m的取值范围; “
,求出函数的最大值,可得m的取值范围; “![]() ”为真,“
”为真,“![]() ”为假,即
”为假,即![]() 与
与![]() 一真一假,分类讨论解出m的范围.
一真一假,分类讨论解出m的范围.
试题解析:
若![]() 为真,则对
为真,则对![]() 恒成立. 设
恒成立. 设![]() ,
,
配方得![]() ,∴
,∴![]() 在
在![]() 上的最小值为-3,∴
上的最小值为-3,∴![]() 解得
解得![]() ,
,
∴![]() 为真时,
为真时, ![]() .若
.若![]() 为真,则
为真,则![]() 成立,即
成立,即![]() 成立.
成立.
设![]() ,则
,则![]() 在
在![]() 上是增函数,∴
上是增函数,∴![]() 的最大值为
的最大值为![]() ,
,
∴![]() ∴
∴![]() 为真时,
为真时, ![]() ∵“
∵“![]() ”为真,“
”为真,“![]() ”为假,∴
”为假,∴![]() 与
与![]() 一真一假.
一真一假.
当![]() 真
真![]() 假时,
假时, 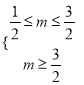 ,∴
,∴![]()
当![]() 假
假![]() 真时,
真时, 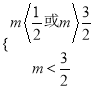 ∴
∴![]()
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.
点睛: 本题考查全特称命题的真假判断以及通过恒成立有解问题转化的函数最值问题.对全称(存在性)命题进行否定的两步操作:①找到命题所含的量词,没有量词的要结合命题的含义加上量词,再进行否定;②对原命题的结论进行否定.判定全称命题“![]() x∈M,p(x)”是真命题,需要对集合M中的每个元素x,证明p(x)成立;要判定一个全称命题是假命题,只要举出集合M中的一个特殊值x0,使p(x0)不成立即可.要判断存在性命题是真命题,只要在限定集合内至少能找到一个x=x0,使p(x0)成立即可,否则就是假命题.
x∈M,p(x)”是真命题,需要对集合M中的每个元素x,证明p(x)成立;要判定一个全称命题是假命题,只要举出集合M中的一个特殊值x0,使p(x0)不成立即可.要判断存在性命题是真命题,只要在限定集合内至少能找到一个x=x0,使p(x0)成立即可,否则就是假命题.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线y2=4x,点M(1,0)关于y轴的对称点为N,直线l过点M交抛物线于A,B两点.
(1)证明:直线NA,NB的斜率互为相反数;
(2)求△ANB面积的最小值;
(3)当点M的坐标为(m,0),(m>0且m≠1).根据(1)(2)推测:△ABC面积的最小值是多少?(不必说明理由)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< ![]() )的部分图象如图所示,下列说法正确的是( )
)的部分图象如图所示,下列说法正确的是( ) 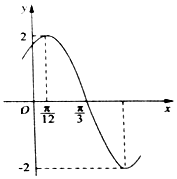
A.函数f(x)的图象关于直线x=﹣ ![]() 对称
对称
B.函数f(x)的图象关于点(﹣ ![]() ,0)对称
,0)对称
C.若方程f(x)=m在[﹣ ![]() ,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣
,0]上有两个不相等的实数根,则实数m∈(﹣2,﹣ ![]() ]
]
D.将函数f(x)的图象向左平移 ![]() 个单位可得到一个偶函数
个单位可得到一个偶函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(1+x)﹣ ![]() . (Ⅰ)若a=2,求f(x)在x=1处的切线方程;
. (Ⅰ)若a=2,求f(x)在x=1处的切线方程;
(Ⅱ)若f(x)≥0对x∈(﹣1,+∞)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中正确的有 . (填上所有正确命题的序号) ①一质点在直线上以速度v=3t2﹣2t﹣1(m/s)运动,从时刻t=0(s)到t=3(s)时质点运动的路程为15(m);
②若x∈(0,π),则sinx<x;
③若f′(x0)=0,则函数y=f(x)在x=x0取得极值;
④已知函数 ![]() ,则
,则 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=sinωx+λcosωx,其图象的一个对称中心到最近的一条对称轴的距离为 ![]() ,且在x=
,且在x= ![]() 处取得最大值.
处取得最大值.
(1)求λ的值.
(2)设 ![]() 在区间
在区间 ![]() 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com