
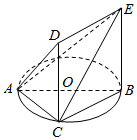
 如图,一简单几何体ABCDE的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.若AC=BC=BE=2,
如图,一简单几何体ABCDE的一个面ABC内接于圆O,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.若AC=BC=BE=2,分析 (1)以CB为x轴,CB为y轴,CD为z轴,建立如图所示的直角坐标系,求出点的坐标,利用直线之间的夹角转化为向量之间的夹角进行求解即可.
(2)设平面BCE的法向量$\overrightarrow{m}$,平面OCE的法向量$\overrightarrow{n}$.二面角O-CE-B是锐二面角,记为θ,利用空间向量的数量积求解cosθ即可.
解答 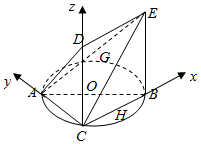 解:(1)以CB为x轴,CA为y轴,CD为z轴,建立如图所示的直角坐标系,
解:(1)以CB为x轴,CA为y轴,CD为z轴,建立如图所示的直角坐标系,
∵AC=BC=BE=2,∴CD=BE=2,
则C(0,0,0),B(2,0,0),A(0,2,0),O(1,1,0),E(2,0,2)
D(0,0,2),
设M(2,0,t),(0≤t≤2),
则$\overrightarrow{AD}$=(0,-2,2),$\overrightarrow{CM}$=(2,0,t),
若AD和CM的夹角为60°,
|cos<$\overrightarrow{AD}$,$\overrightarrow{CM}$>|=|$\frac{\overrightarrow{AD}•\overrightarrow{CM}}{|\overrightarrow{AD}||\overrightarrow{CM}|}$|=|$\frac{2t}{\sqrt{4+4}•\sqrt{4+{t}^{2}}}$|=|$\frac{t}{\sqrt{2}•\sqrt{4+{t}^{2}}}$|=cos60$°=\frac{1}{2}$,
平方得t2=4,得t=2,
即M(2,0,2),即M位于E处时,AD和CM的夹角为60°.
(2)设平面OCE的法向量$\overrightarrow{n}$=(x0.y0.z0).则平面BCE的法向量$\overrightarrow{m}$=(0,1,0),
$\overrightarrow{CE}$=(2,0,2),$\overrightarrow{CO}$=(1,1,0).
∴$\left\{\begin{array}{l}\overrightarrow{n}•\overrightarrow{CE}=0\\ \overrightarrow{n}•\overrightarrow{CO}=0\end{array}\right.$,则$\left\{\begin{array}{l}2{x}_{0}+2{z}_{0}=0\\{x}_{0}+{y}_{0}=0\end{array}\right.$,
令x0=-1,∴$\overrightarrow{n}$=(-1,1,1).
∵二面角O-CE-B是锐二面角,记为θ,则
cosθ=|cos$<\overrightarrow{m},\overrightarrow{n}>$|=$\frac{\overrightarrow{m}•\overrightarrow{n}}{\left|\overrightarrow{m}\right|\left|\overrightarrow{n}\right|}$=$\frac{1}{1×\sqrt{3}}$=$\frac{\sqrt{3}}{3}$.
点评 本题主要考查空间角的计算,根据异面直线所成角转化为向量之间的夹角以及求出平面的法向量利用向量法求二面角是解决本题的关键.注意向量法的应用.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|$\frac{1}{2}$<x<3} | B. | {x|x<$\frac{1}{2}$或x>3} | C. | {x|-$\frac{1}{2}$<x<3} | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | 0 | D. | -2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com