
已知 为坐标原点,且
为坐标原点,且 ,则
,则 点的坐标为 .
点的坐标为 .
科目:高中数学 来源: 题型:
(本小题满分12分)已知![]() 为坐标原点,向量
为坐标原点,向量![]() ,点是直线
,点是直线![]() 上的一点,且点分有向线段
上的一点,且点分有向线段![]() 的比为.(1)记函数
的比为.(1)记函数![]() ,
,![]() ,讨论函数
,讨论函数![]() 的单调性,并求其值域;(2)若
的单调性,并求其值域;(2)若![]() 三点共线,求
三点共线,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题满分18分,其中第1小题5分,第2小题5分,第3小题8分)
在平面直角坐标系中,已知![]() 为坐标原点,点
为坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,其中
,其中![]() 且
且![]() .设
.设![]() .
.
(1)若![]() ,
,![]() ,
,![]() ,求方程
,求方程![]() 在区间
在区间![]() 内的解集;
内的解集;
(2)若点![]() 是过点
是过点![]() 且法向量为
且法向量为![]() 的直线
的直线![]() 上的动点.当
上的动点.当![]() 时,设函数
时,设函数![]() 的值域为集合
的值域为集合![]() ,不等式
,不等式![]() 的解集为集合
的解集为集合![]() . 若
. 若![]() 恒成立,求实数
恒成立,求实数![]() 的最大值;
的最大值;
(3)根据本题条件我们可以知道,函数![]() 的性质取决于变量
的性质取决于变量![]() 、
、![]() 和
和![]() 的值. 当
的值. 当![]() 时,试写出一个条件,使得函数
时,试写出一个条件,使得函数![]() 满足“图像关于点
满足“图像关于点![]() 对称,且在
对称,且在![]() 处
处![]() 取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
取得最小值”.(说明:请写出你的分析过程.本小题将根据你对问题探究的完整性和在研究过程中所体现的思维层次,给予不同的评分.)
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)已知![]() 为坐标原点,
为坐标原点,![]() 其中
其中![]() 为常数,设函数
为常数,设函数![]() .
.
(1)求函数![]() 的表达式和最小正周期;
的表达式和最小正周期;
(2)若角![]() 为
为![]() 的三个内角中的最大角且
的三个内角中的最大角且![]() 的最小值为
的最小值为![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,试画出![]() 的简图.
的简图.
查看答案和解析>>
科目:高中数学 来源:广州省2009-2010学年高二学科竞赛(数学理) 题型:解答题
(本小题满分14分)已知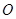 为坐标原点,点F、T、M、P分别满足
为坐标原点,点F、T、M、P分别满足 .
.
(1) 当t 变化时,求点P的轨迹方程;
(2) 若 的顶点在点P的轨迹上,且点A的纵坐标
的顶点在点P的轨迹上,且点A的纵坐标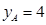 ,
, 的重心恰好为点F,
的重心恰好为点F,
求直线BC的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com