练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知向量＝(cos25°,sin25°)，＝(sin20°,cos20°)，若t是实数，且＝＋t，则||的最小值为                          （    ）

    A．    B．1       C．    D．

    C


    解析:

    ||2＝||2＋t2||2＋2t·＝1＋t2＋2t(sin20°cos25°＋cos20°sin25°)＝t2＋t＋1＝(t＋)2＋，||＝，∴||min＝.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：山东省泰安市2012届高三上学期期中考试数学理科试题 题型：044

    已知向量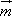＝(1，－2)与(1，λ)．

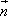    (Ⅰ)若在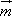方向上的投影为，求λ的值；

    (Ⅱ)命题P：向量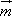与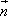的夹角为锐角；

    命题q：＝2，其中向量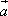＝(λ＋2，λ2－cos2α)

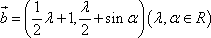    ．若“p或q”为真命题，“p且q”为假命题，求λ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：黑龙江省牡丹江一中2012届高三上学期期中考试数学文科试题 题型：044

    已知向量＝(sin，1)，＝(cos，cos2)

    (1)若·＝1，求cos(－x)的值

    (2)记f(x)＝·，在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cosB＝bcosC，求函数f(A)的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：江西省2012届高三第一次五校联考数学理科试卷 题型：044

    已知向量＝(sin，1)，＝(cos，cos2)

    (Ⅰ)若·＝1，求cos(－x)的值；

    (Ⅱ)记f(x)＝·，在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cosB＝bcosC，求函数f(A)的取值范围．

    查看答案和解析>>

    科目：高中数学 来源：吉林省长春市实验中学2012届高三模拟考试数学文科试题 题型：044

    已知向量＝(1＋sin2x，sinx－cosx)，＝(1，sinx＋cos)，函数f(x)＝·

    (1)求函数f(x)的最大值及相应的x的值；

    (2)若f()＝，求cos2(－2)的值．

    查看答案和解析>>

    科目：高中数学 来源：2015届湖南省高一4月段考数学试卷（解析版） 题型：解答题

    已知向量＝(sin，1)，＝(cos，cos2)

    (1)若·＝1，求cos(－x)的值；

    (2)记f(x)＝·，在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cosB＝bcosC，求函数f(A)的取值范围．

     

    查看答案和解析>>

    同步练习册答案