已知函数f(x)=(x2+ax+b)ex,且f(0)=7,x=1是它的极值点.
(1)求f(x)的表达式;
(2)试确定f(x)的单调区间;
(3)若函数g(x)=f(x)-m(m∈R)恰有3个零点,求m的取值范围.
解:(1)∵f(0)=7,∴b=7.
又f′(x)=[x
2+(2+a)x+a+b]e
x,x=1是f(x)的极值点,
∴f′(1)=0,即(10+2a)e=0,∴a=-5,
∴f(x)=(x
2-5x+7)e
x;
(2)∵f′(x)=(x
2-3x+2)e
x=(x-1)(x-2)e
x令f′(x)>0得x<1或x>2;令f′(x)<0得1<x<2,
∴f(x)的单调增区间为(-∞,1)和(2,+∞),f(x)的单调减区间为(1,2);
(3)由(2)知f(x)
最大=f(1)=3e,f(x)
最小=f(2)=e
2.
若g(x)=f(x)-m(m∈R)恰有3个零点,则只需y=f(x)与y=m的图象有三个交点.
由于f(x)在(-∞,1)单调递增,且f(-1)=
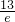
<f(2),
故只要f(x)
最小<m<f(x)
最大,∴e
2<m<3e.
故当e
2<m<3e时,g(x)=f(x)-m(m∈R)恰有3个零点.
分析:(1)把x等于0代入函数解析式让其等于7即可解出b的值,然后求f(x)的导函数,因为x等于1是函数的极值点,所以把x等于1代入到到函数中即可求出a的值,把a的值和b的值代入到f(x)中得到f(x)的解析式;
(2)把a与b代入到函数的导函数中,分解因式后,令导函数大于0解出x的范围即为函数的增区间,令导函数小于0解出x的范围即为函数的减区间;
(3)根据(2)得到的函数单调区间,根据函数的增减性得到函数的最大值和最小值,若g(x)=f(x)-m(m∈R)恰有3个零点,则只需y=f(x)与y=m的图象有三个交点,即要m大于函数的最小值,小于函数的最大值,即可求出符合题意m的范围.
点评:此题考查学生会根据导函数的正负判断函数的单调性,并根据函数的增减性得到函数的最值,掌握函数的零点与方程交点的关系,是一道中档题.

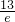 <f(2),
<f(2),
