练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知二次函数f(x)＝x2－bx＋c，f(0)＝4，f(1＋x)＝f(1－x)，则(　　)

    A．f(bx)≥f(cx) B．f(bx)≤f(cx)

    C．f(bx)>f(cx) D．f(bx)<f(cx)

     

    B

    【解析】由f(0)＝4，得c＝4，由f(1＋x)＝f(1－x)，知二次函数f(x)图象的对称轴为x＝1，即＝1，即b＝2，故f(x)＝x2－2x＋4，bx＝2x，cx＝4x. 当x≥0时，cx≥bx≥1，而二次函数f(x)在(1，＋∞)上单调递增，故f(bx)≤f(cx)；当x<0时，0<cx<bx<1，而二次函数f(x)在(－∞，1)上单调递减，故f(bx)<f(cx)．综上可知选B.

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-9函数模型及其应用（解析版） 题型：选择题

    某种商品进价为每件100元，按进价增加25%出售，后因库存积压降价，按九折出售，每件还获利(　　)

    A．25元 B．20.5元 C．15元 D．12.5元

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-6对数与对数函数（解析版） 题型：填空题

    已知函数f(x)＝ln(1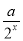－)的定义域是(1，＋∞)，则实数a的值为________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-5指数及指数函数（解析版） 题型：选择题

    设a＝40.8，b＝80.46，c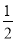＝()－1.2，则a，b，c的大小关系为(　　)

    A．a>b>c B．b>a>c C．c>a>b D．c>b>a

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：解答题

    已知函数f(x)＝xm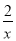－且f(4)＝.

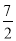    (1)求m的值；

    (2)判定f(x)的奇偶性；

    (3)判断f(x)在(0，＋∞)上的单调性，并给予证明．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-4二次函数与幂函数（解析版） 题型：选择题

    若函数y＝ax与y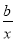＝－在(0，＋∞)上都是减函数，则y＝ax2＋bx在(0，＋∞)上(　　)

    A．单调递增 B．单调递减

    C．先增后减 D．先减后增

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-3函数的奇偶性与周期性（解析版） 题型：解答题

    设f(x)是(－∞，＋∞)上的奇函数，f(x＋2)＝－f(x)，当0≤x≤1时，f(x)＝x.

    (1)求f(π)的值；

    (2)当－4≤x≤4时，求f(x)的图象与x轴所围图形的面积．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-2函数的单调性与最值（解析版） 题型：填空题

    函数y＝在(－2，＋∞)上为增函数，则a的取值范围是________．

     

    查看答案和解析>>

    科目：高中数学 来源：2015高考数学（理）一轮配套特训：2-11导数的应用一（解析版） 题型：解答题

    已知函数f(x)＝(x2＋ax－2a2＋3a)ex(x∈R)，其中a∈R.

    (1)当a＝0时，求曲线y＝f(x)在点(1，f(1))处的切线的斜率；

    (2)当a≠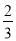时，求函数y＝f(x)的单调区间与极值．

     

    查看答案和解析>>

    同步练习册答案