
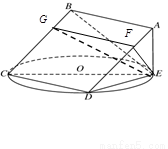
如图,正方形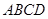 所在平面与圆
所在平面与圆 所在平面相交于
所在平面相交于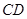 ,线段
,线段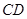 为圆
为圆 的弦,
的弦,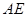 垂直于圆
垂直于圆 所在平面,垂足
所在平面,垂足 是圆
是圆 上异于
上异于 、
、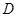 的点,
的点, ,圆
,圆 的直径为9。
的直径为9。
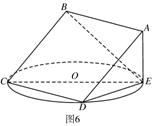
(1)求证:平面 平面
平面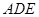 ;
;
(2)求二面角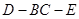 的平面角的正切值。
的平面角的正切值。
(1)证明见解析 (2)二面角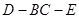 的平面角的正切值为
的平面角的正切值为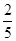 。
。
【解析】本试题主要是考查了立体几何中面面垂直的判定和二面角的求解的综合运用。
(1)要证明面面垂直,只要证明线面垂直,再结合面面垂直的判定定理得到结论。
(2)合理的建立空间直角坐标系,然后求解得到平面的法向量和法向量,运用向量的夹角公式得到二面角的平面角的求解。
(1)证明:∵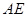 垂直于圆
垂直于圆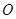 所在平面,
所在平面,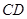 在圆
在圆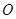 所在平面上,
所在平面上,
∴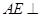
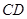 。
。
在正方形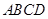 中,
中,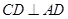 ,
,
∵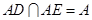 ,∴
,∴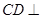 平面
平面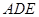 .∵
.∵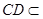 平面
平面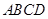 ,
,
∴平面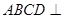 平面
平面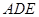 。 ……………………………………………6分
。 ……………………………………………6分
(2)解法1:
∵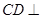 平面
平面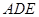 ,
,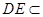 平面
平面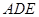 ,
,
∴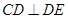 。
。
∴ 为圆
为圆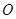 的直径,即
的直径,即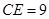 .
.
设正方形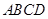 的边长为
的边长为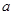 ,
,
在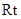 △
△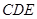 中,
中,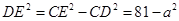 ,
,
在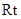 △
△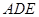 中,
中,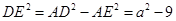 ,
,
由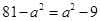 ,解得,
,解得,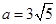 。 ∴
。 ∴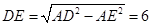 。
。
过点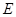 作
作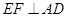 于点
于点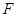 ,作
,作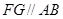 交
交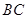 于点
于点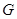 ,连结
,连结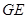 ,
,
由于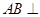 平面
平面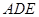 ,
,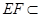 平面
平面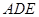 ,∴
,∴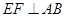 。∵
。∵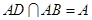 ,
,
∴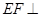 平面
平面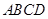 。∵
。∵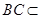 平面
平面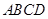 ,
,
∴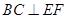 。∵
。∵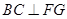 ,
,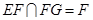 ,
,
∴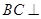 平面
平面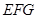 。∵
。∵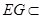 平面
平面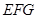 ,∴
,∴ 。
。
∴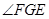 是二面角
是二面角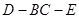 的平面角。…………………………………10分
的平面角。…………………………………10分
在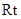 △
△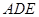 中,
中,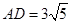 ,
,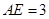 ,
,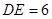 ,
,
∵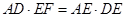 ,∴
,∴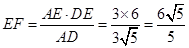 。
。
在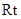 △
△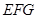 中,
中,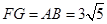 ,∴
,∴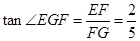 。
。
故二面角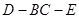 的平面角的正切值为
的平面角的正切值为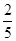 。 …………………………12分
。 …………………………12分
解法2:∵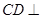 平面
平面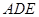 ,
,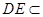 平面
平面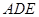 ,
,
∴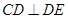 。∴
。∴ 为圆
为圆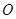 的直径,即
的直径,即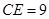 。
。
设正方形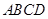 的边长为
的边长为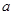 ,在
,在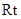 △
△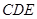 中,
中,
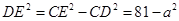 ,
,
在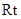 △
△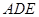 中,
中,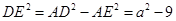 ,
,
由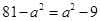 ,解得,
,解得,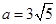 。∴
。∴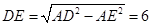 。
。
以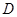 为坐标原点,分别以
为坐标原点,分别以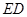 、
、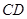 所在的直线为
所在的直线为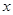 轴、
轴、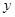 轴建立如图所示的空间直角坐标系,
轴建立如图所示的空间直角坐标系,

则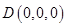 ,
,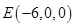 ,
,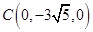 ,
,
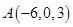 ,
, 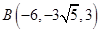 。……………8分
。……………8分
设平面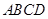 的法向量为
的法向量为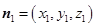 ,
,
则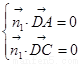 即
即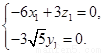
取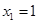 ,则
,则 是平面
是平面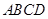 的一个法向量。…………9分
的一个法向量。…………9分
设平面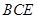 的法向量为
的法向量为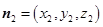 ,则
,则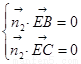 即
即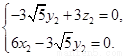
取 ,则
,则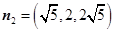 是平面
是平面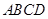 的一个法向量。…………10分
的一个法向量。…………10分
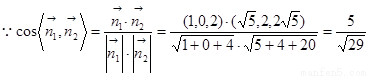 ,
,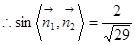 .
.
∴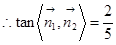
故二面角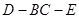 的平面角的正切值为
的平面角的正切值为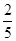


科目:高中数学 来源: 题型:
(本小题满分12分)如图,正方形![]() 所在平面与平面四边形
所在平面与平面四边形![]() 所在平面互相垂直,△
所在平面互相垂直,△![]() 是等腰直角三角形,
是等腰直角三角形,![]() 。
。
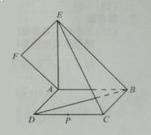
(Ⅰ)求证:![]() ;
;
(Ⅱ)设线段![]() 的中点为
的中点为![]() ,在直线
,在直线![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() ?若存在,请指出点
?若存在,请指出点![]() 的位置,并证明你的结论;若不存在,请说明理由;
的位置,并证明你的结论;若不存在,请说明理由;
(Ⅲ)求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
如图,正方形![]() 所在平面与平面四边形
所在平面与平面四边形![]() 所在平面互相垂直,△
所在平面互相垂直,△![]() 是等腰直角三角形,
是等腰直角三角形,![]() 。
。
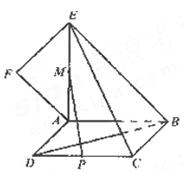
(Ⅰ)求证:![]() ;
;
(Ⅱ)设线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,求证:
,求证:![]() ∥
∥![]()
(Ⅲ)求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009四川卷文)(本小题满分12分)
如图,正方形![]() 所在平面与平面四边形
所在平面与平面四边形![]() 所在平面互相垂直,△
所在平面互相垂直,△![]() 是等腰直角三角形,
是等腰直角三角形,![]()
(I)求证:![]() ;
;
(II)设线段![]() 、
、![]() 的中点分别为
的中点分别为![]() 、
、![]() ,求证:
,求证: ![]() ∥
∥![]()
 (III)求二面角
(III)求二面角![]() 的大小。
的大小。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年辽宁省丹东市四校协作体高三第二次联合考试理科数学卷 题型:解答题
(本小题满分12分)
如图,正方形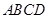 所在平面与圆
所在平面与圆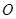 所在平面相交于
所在平面相交于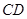 ,线段
,线段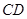 为圆
为圆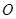 的弦,
的弦,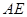 垂直于圆
垂直于圆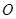 所在平面,垂足
所在平面,垂足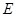 是圆
是圆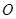 上异于
上异于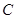 .
.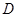 的点,
的点,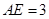 ,圆
,圆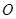 的直径为9.
的直径为9.
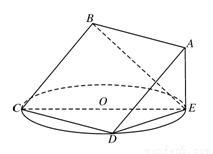
(I)求证:平面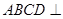 平面
平面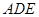 ;
;
(II)求二面角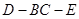 的平面角的正切值.
的平面角的正切值.
查看答案和解析>>
科目:高中数学 来源:2010年山西省高一上学期期中考试数学试卷 题型:解答题
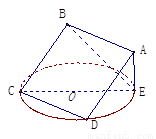
如图,正方形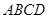 所在平面与圆
所在平面与圆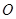 所在平面相交于
所在平面相交于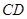 ,线段
,线段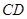 为圆
为圆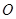 的弦,
的弦,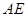 垂直于圆
垂直于圆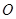 所在平面,垂足
所在平面,垂足 是圆
是圆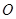 上异于
上异于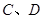 的点,
的点,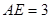 ,圆
,圆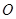 的直径为
的直径为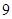 ,
,
1)求证:平面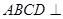 平面
平面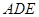 2)求二面角
2)求二面角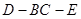 的平面角的正切值.(12分)
的平面角的正切值.(12分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com