练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （5分）（2011•湖北）某市有大型超市200家、中型超市400家、小型超市1400家．为掌握各类超市的营业情况，现按分层抽样方法抽取一个容量为100的样本，应抽取中型超市          家．
    20

    试题分析：根据所给的三种超市的数目，相加得到共有的超市数目，根据要抽取的超市数目，得到每个个体被抽到的概率，用中等超市的数目乘以被抽到的概率，得到结果．
    解：∵大型超市200家、中型超市400家、小型超市1400家，
    ∴共有超市200+400+1400=2000，
    ∵按分层抽样方法抽取一个容量为100的样本，
    ∴每个个体被抽到的概率是，
    ∴中型超市要抽取400×=20家，
    故答案为：20．
    点评：本题考查分层抽样，这是一个每年必考的题目，解题的关键是抽样过程中每个个体被抽到的概率相等．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    某单位有2000名职工，老年、中年、青年分布在管理、技术开发、营销、生产各部门中，如下表所示：
    人数
    		管理
    		技术开发
    		营销
    		生产
    		共计
    老年
    		40
    		40
    		40
    		80
    		200
    中年
    		80
    		120
    		160
    		240
    		600
    青年
    		40
    		160
    		280
    		720
    		1 200
    小计
    		160
    		320
    		480
    		1 040
    		2 000
    (1)若要抽取40人调查身体状况，则应怎样抽样？
    (2)若要开一个25人的讨论单位发展与薪金调整方面的座谈会，则应怎样抽选出席人？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如图，⊙O1与⊙O2相交于A、B两点，AB是⊙O2的直径，过A点作⊙O1的切线交⊙O2于点E，并与BO1的延长线交于点P，PB分别与⊙O1、⊙O2交于C，D两点．
    求证：
    （1）PA•PD=PE•PC；
    （2）AD=AE．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某学校共有教职工900人，分成三个批次进行继续教育培训，在三个批次中男、女教职工人数如下表所示．已知在全体教职工中随机抽取1名，抽到第二批次中女教职工的概率是0．16．
     
    		第一批次
    		第二批次
    		第三批次
    女教职工
    		196
    		x
    		y
    男教职工
    		204
    		156
    		z
     
    (1)求x的值；
    (2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查，问应在第三批次中抽取教职工多少名？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

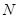    对一个容量为的总体抽取容量为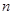的样本，当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时，总体中每个个体被抽中的概率分别为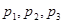，则（  ）
    A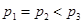．B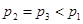．C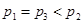．D．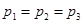

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    [2014·天津模拟]某校对全校1600名男女学生的视力状况进行调查，现用分层抽样的方法抽取一个容量为200的样本，已知女生比男生少抽10人，则该校的女生人数应该为________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某单位有27名老年人， 54名中年人，81名青年人. 为了调查他们的身体情况，用分层抽样的方法从他们中抽取了n个人进行体检，其中有6名老年人，那么n=（  ）
    A．35B．36C．37D．162

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    某单位有840名职工，现采用系统抽样方法，抽取42人做问卷调查，将840人按1,2，…，840随机编号，则抽取的42人中，编号落入区间[481, 720]的人数为(　　)
    A．11B．12C．13D．14

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    将容量为n的样本中的数据分成6组，绘制成频率分布直方图，若第一组至第六组数据的频率之比为2:3:4:6:4:1，且前三组数据的频率之和等于27，则n等于        .

    查看答案和解析>>

    同步练习册答案