
|
(1)证明:![]() 平面
平面![]()

![]()

|
|
|
|
|
|
|
|
(1)证明:连结AD1交A1D于O,连结EO,则O为AD1的中点,又因为E是AB的中点,
所以OE∥BD1.
又∵![]() 平面A1DE BD1
平面A1DE BD1![]() 平面A1DE ∴BD1∥平面A1DE ……………………4分
平面A1DE ∴BD1∥平面A1DE ……………………4分
(2)证明:由题可知:四边形ADD1A1是正方形
∴A1D⊥AD1 又∵AB⊥平面ADD1A1,A1D![]() 平面ADD1A1
平面ADD1A1
∴AB⊥AD1 又∵AB![]() 平面AD1E,AD1
平面AD1E,AD1![]() 平面A D1E AB
平面A D1E AB![]() AD1=A
AD1=A
∴A1D⊥平面AD1E 又∵D1E![]() 平面AD1E ∴A1D⊥D1E ………………………8分
平面AD1E ∴A1D⊥D1E ………………………8分
(3)解:在△CED中,CD=2,![]() ,
,![]()
CD2=CE2+DE2 ∴CE⊥DE。
又∵D1D⊥平面ABCD CE![]() 平面ABCD ∴CE⊥D1D
平面ABCD ∴CE⊥D1D
又∵![]() 平面D1DE DE
平面D1DE DE![]() 平面D1DE D1D
平面D1DE D1D![]() DE=D
DE=D
∴CE⊥平面D1DE 又∵D1E⊥平面D1DE,∴CE⊥D1E.
∴∠D1ED是二面角D1—ED—D的一个平面角.
在△D1ED中,∠D1DE=90°,D1D=1, DE=![]()
∴![]() ∴二面角D1—ED—D的正切值是
∴二面角D1—ED—D的正切值是![]() …………12分
…………12分


 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
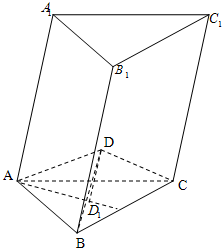 已知三棱锥D-ABC,D1为底面△ABC的重心,过A、B、C分别作DD1的平行线分别交对面所在的平面于A1,B1,C1点.(如,过A点作DD1的平行线交BCD所在的平面于A1点)
已知三棱锥D-ABC,D1为底面△ABC的重心,过A、B、C分别作DD1的平行线分别交对面所在的平面于A1,B1,C1点.(如,过A点作DD1的平行线交BCD所在的平面于A1点)查看答案和解析>>
科目:高中数学 来源: 题型:
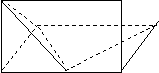
 (2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.
(2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.| 1 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
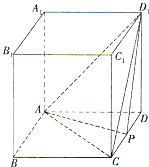 如图,正方体ABCD-A1B1C1D1的棱长为2,P为棱CD上的一点,且三棱锥A-CP D1的体积为
如图,正方体ABCD-A1B1C1D1的棱长为2,P为棱CD上的一点,且三棱锥A-CP D1的体积为| 2 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com