
 ,则
,则 是函数
是函数 的极值点,因为
的极值点,因为 中,
中, 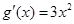 且
且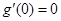 ,所以0是
,所以0是 的极值点.”在此“三段论”中,下列说法正确的是( )
的极值点.”在此“三段论”中,下列说法正确的是( )| A.推理过程错误 | B.大前提错误 | C.小前提错误 | D.大、小前提错误 |
科目:高中数学 来源:不详 题型:单选题
| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,
, ,
, ,
, 都是质数,于是他提出猜想:任何形如
都是质数,于是他提出猜想:任何形如 N*)的数都是质数,这就是著名的费马猜想. 半个世纪之后,善于发现的欧拉发现第5个费马数
N*)的数都是质数,这就是著名的费马猜想. 半个世纪之后,善于发现的欧拉发现第5个费马数 不是质数,从而推翻了费马猜想,这一案例说明( )
不是质数,从而推翻了费马猜想,这一案例说明( )| A.归纳推理,结果一定不正确 | B.归纳推理,结果不一定正确 |
| C.类比推理,结果一定不正确 | D.类比推理,结果不一定正确 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

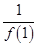 +
+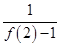 +
+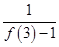 +…+
+…+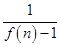 的值.
的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com