
在底面半径为6的圆柱内,有两个半径也为6的球面,两球的球心距为13,若作一个平面与两个球都相切,且与圆柱面相交成一椭圆,则椭圆的长轴长为 .
13
【解析】
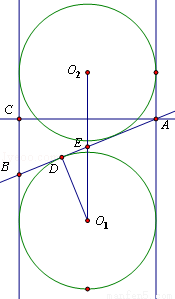
试题分析:设两个球的球心分别为O1、O2,椭圆的长轴为AB,作出由AB与O1O2确定平面α与两个球及圆柱的截面,并过A作O1O2的垂线,交圆柱的母线于点C,连接O1与AB切球O1的切点D.分别在Rt△O1DE中和Rt△ABC中,利用∠BAC=∠DO1E和余弦的定义,结合题中的数据建立关系式,即可解出AB的长,即得该椭圆的长轴长.
【解析】
设两个球的球心分别为O1、O2,所得椭圆的长轴为AB,
直线AB与O1O2交于点E,设它们确定平面α,
作出平面α与两个球及圆柱的截面,如图所示
过A作O1O2的垂线,交圆柱的母线于点C,设AB切球O1的大圆于点D,连接O1D
∵Rt△O1DE中,O1E=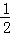 O1O2=
O1O2=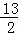 ,O1D=6
,O1D=6
∴cos∠DO1E=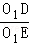 =
=
∵锐角∠DO1E与∠BAC的两边对应互相垂直
∴∠BAC=∠DO1E,
得Rt△ABC中,cos∠BAC=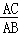 =
=
∵AC长等于球O1的直径,得AC=12
∴椭圆的长轴AB=13
故答案为:13


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源:2014-2015学年安徽省淮北市高三第一次模拟考试理科数学试卷(解析版) 题型:选择题
已知棱长为1的正方体的俯视图是边长为1正方形,则其主视图的面积不可能是( )
A. B.
B.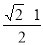 C. 1 D.
C. 1 D.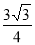
查看答案和解析>>
科目:高中数学 来源:2014-2015学年上海市高二上学期第一次月考数学试卷(解析版) 题型:填空题
设数列 的前
的前 项和为
项和为 ,关于数列
,关于数列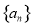 有下列三个命题:
有下列三个命题:
①若 即是等差数列,又是等比数列,则
即是等差数列,又是等比数列,则
②若 ,则
,则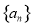 是等差数列;
是等差数列;
③若 ,则
,则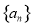 是等比数列
是等比数列
这些命题中,真命题的序号是_____________.
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.3柱面与平面的截面练习卷(解析版) 题型:填空题
底面直径为12cm的圆柱被与底面成30°的平面所截,截口是一个椭圆,该椭圆的长轴长 8 cm ,短轴长 ,离心率为 .
cm ,短轴长 ,离心率为 .

查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:填空题
(2011•成都二模)如图,在半径为l的球O中.AB、CD是两条互相垂直的直径,半径OP⊥平面ACBD.点E、F分别为大圆上的劣弧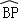 、
、 的中点,给出下列结论:
的中点,给出下列结论:
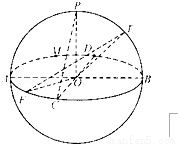
①E、F两点的球面距离为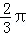 ;
;
②向量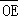 在向量
在向量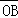 方向上的投影恰为
方向上的投影恰为 ;
;
③若点M为大圆上的劣弧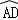 的中点,则过点M且与直线EF、PC成等角的直线有无数条;
的中点,则过点M且与直线EF、PC成等角的直线有无数条;
④球面上到E、F两点等距离的点的轨迹是两个点;
其中你认为正确的所有结论的序号为 .
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修4-1 2.2直线与球、平面与球位置关系(解析版) 题型:选择题
(2011•邢台一模)设有平面α,β,γ两两互相垂直,且α,β,γ三个平面有一个公共点A,现有一个半径为1的小球与α,β,γ这三个平面均相切,则小球上任一点到点A的最近距离为( )
A.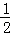 B.
B.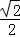 C.
C.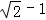 D.
D.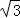 ﹣1
﹣1
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修2-2 2.5简单复合函数求导法则练习卷(解析版) 题型:?????
(2014•榆林模拟)要得到函数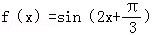 的导函数f′(x)的图象,只需将f(x)的图象( )
的导函数f′(x)的图象,只需将f(x)的图象( )
A.向右平移 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)
个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)
B.向左平移 个单位,再把各点的纵坐标缩短到原来的2倍(横坐标不变)
个单位,再把各点的纵坐标缩短到原来的2倍(横坐标不变)
C.向右平移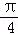 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)
个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)
D.向左平移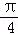 个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)
个单位,再把各点的纵坐标伸长到原来的2倍(横坐标不变)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com