
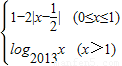 ,若方程f(x)=m存在三个不等的实根x1,x2,x3,则x1+x2+x3的取值范围是( )
,若方程f(x)=m存在三个不等的实根x1,x2,x3,则x1+x2+x3的取值范围是( ) 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(2009•普宁市模拟)为了确保神州七号飞船发射时的信息安全,信息须加密传输,发送方由明文→密文(加密),接受方由密文→明文(解密),已知加密的方法是:密码把英文的明文(真实文)按字母分解,其中英文的a,b,c,…,z的26个字母(不论大小写)依次对应1,2,3,…,26这26个自然数(见下表):
|
查看答案和解析>>
科目:高中数学 来源:普宁市模拟 题型:单选题
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | w | x | y | z |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 10 | 21 | 22 | 23 | 24 | 25 | 26 |
|
| 8 |
| 2 |
| 5+1 |
| 2 |
| A.love | B.live | C.move | D.life |
查看答案和解析>>
科目:高中数学 来源:河北省模拟题 题型:解答题
 是否有实数解.
是否有实数解.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com