
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌШчЙћxгыyЖМЪЧећЪ§ЃЌОЭГЦЕуЃЈxЃЌyЃЉЮЊећЕуЃЌЯТСаУќЬтжае§ШЗЕФЪЧЃЈаДГіЫљгае§ШЗУќЬтЕФБрКХЃЉ
ЂйДцдкетбљЕФжБЯпЃЌМШВЛгызјБъжсЦНаагжВЛОЙ§ШЮКЮећЕуЃЛ
ЂкШчЙћkгыbЖМЪЧЮоРэЪ§ЃЌдђжБЯпy=kx+bВЛОЙ§ШЮКЮећЕуЃЛ
ЂлШчЙћжБЯпlОЙ§СНИіВЛЭЌЕФећЕуЃЌдђжБЯпlБиОЙ§ЮоЧюЖрИіећЕуЃЛ
ЂмжБЯпy=kx+bОЙ§ЮоЧюЖрИіећЕуЕФГфЗжБивЊЬѕМўЪЧЃКkгыbЖМЪЧгаРэЪ§ЃЛ
ЂнДцдкЧЁОЙ§вЛИіећЕуЕФжБЯпЃЎ
ЁОД№АИЁПЂйЂлЂн
ЁОНтЮіЁПНтЃКЂйСюy=x+ ![]() ЃЌМШВЛгызјБъжсЦНаагжВЛОЙ§ШЮКЮећЕуЃЌЫљвдБОУќЬте§ШЗЃЛЂкШєk=
ЃЌМШВЛгызјБъжсЦНаагжВЛОЙ§ШЮКЮећЕуЃЌЫљвдБОУќЬте§ШЗЃЛЂкШєk= ![]() ЃЌb=
ЃЌb= ![]() ЃЌдђжБЯпy=
ЃЌдђжБЯпy= ![]() x+
x+ ![]() ОЙ§ЃЈЉ1ЃЌ0ЃЉЃЌЫљвдБОУќЬтДэЮѓЃЛ
ОЙ§ЃЈЉ1ЃЌ0ЃЉЃЌЫљвдБОУќЬтДэЮѓЃЛ
Щшy=kxЮЊЙ§дЕуЕФжБЯпЃЌШєДЫжБЯпlЙ§ВЛЭЌЕФећЕуЃЈx1 ЃЌ y1ЃЉКЭЃЈx2 ЃЌ y2ЃЉЃЌ
АбСНЕуДњШыжБЯпlЗНГЬЕУЃКy1=kx1 ЃЌ y2=kx2 ЃЌ
СНЪНЯрМѕЕУЃКy1Љy2=kЃЈx1Љx2ЃЉЃЌ
дђЃЈx1Љx2 ЃЌ y1Љy2ЃЉвВдкжБЯпy=kxЩЯЧвЮЊећЕуЃЌ
ЭЈЙ§етжжЗНЗЈЕУЕНжБЯпlОЙ§ЮоЧюЖрИіећЕуЃЌдђЂле§ШЗЃЛ
ЂмЕБkЃЌbЖМЮЊгаРэЪ§ЪБЃЌy=kx+bПЩФмВЛОЙ§ећЕуЃЌР§Шчk= ![]() ЃЌb=
ЃЌb= ![]() ЃЌЙЪЂмВЛе§ШЗЃЛ
ЃЌЙЪЂмВЛе§ШЗЃЛ
ЂнСюжБЯпy= ![]() xЧЁОЙ§ећЕуЃЈ0ЃЌ0ЃЉЃЌЫљвдБОУќЬте§ШЗЃЎ
xЧЁОЙ§ећЕуЃЈ0ЃЌ0ЃЉЃЌЫљвдБОУќЬте§ШЗЃЎ
злЩЯЃЌУќЬте§ШЗЕФађКХгаЃКЂйЂлЂнЃЎ
ЫљвдД№АИЪЧЃКЂйЂлЂнЃЎ
ЁОПМЕуОЋЮіЁПеЦЮеУќЬтЕФецМйХаЖЯгыгІгУЪЧНтД№БОЬтЕФИљБОЃЌашвЊжЊЕРСНИіУќЬтЛЅЮЊФцЗёУќЬтЃЌЫќУЧгаЯрЭЌЕФецМйадЃЛСНИіУќЬтЮЊЛЅФцУќЬтЛђЛЅЗёУќЬтЃЌЫќУЧЕФецМйадУЛгаЙиЯЕЃЎ


 УћЪІЕуОІзжДЪОфЖЮЦЊЯЕСаД№АИ
УћЪІЕуОІзжДЪОфЖЮЦЊЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌдкЖрУцЬх![]() жаЃЌ
жаЃЌ![]() ЪЧБпГЄЮЊ2ЕФЕШБпШ§НЧаЮЃЌ
ЪЧБпГЄЮЊ2ЕФЕШБпШ§НЧаЮЃЌ![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЃЎ
ЃЎ

ЃЈ1ЃЉШєЦНУц![]() ЦНУц
ЦНУц![]() ЃЌжЄУїЃК
ЃЌжЄУїЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШє![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕНЦНУц
ЕНЦНУц![]() ЕФОрРыЃЎ
ЕФОрРыЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌЩфЯпy=xЃЈxЁн0ЃЉКЭy=0ЃЈxЁн0ЃЉЩЯЗжБ№вРДЮгаЕуA1ЁЂA2 ЃЌ ЁЃЌAn ЃЌ ЁЃЌКЭЕуB1 ЃЌ B2 ЃЌ ЁЃЌBnЁЃЌЦфжа ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЎЧв
ЃЎЧв ![]() ЃЌ
ЃЌ ![]() ЃЈn=2ЃЌ3ЃЌ4ЁЃЉЃЎ
ЃЈn=2ЃЌ3ЃЌ4ЁЃЉЃЎ 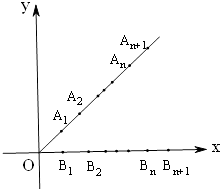
ЃЈ1ЃЉгУnБэЪО|OAn|МАЕуAnЕФзјБъЃЛ
ЃЈ2ЃЉгУnБэЪО|BnBn+1|МАЕуBnЕФзјБъЃЛ
ЃЈ3ЃЉаДГіЫФБпаЮAnAn+1Bn+1BnЕФУцЛ§ЙигкnЕФБэДяЪНSЃЈnЃЉЃЌВЂЧѓSЃЈnЃЉЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() ЃЌ
ЃЌ ![]() ЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЮЊздШЛЖдЪ§ЕФЕзЪ§.
ЃЈIЃЉШєЧњЯп![]() дкЕу
дкЕу![]() ДІЕФЧаЯпЦНаагк
ДІЕФЧаЯпЦНаагк![]() жс,Чѓ
жс,Чѓ![]() ЕФжЕ;
ЕФжЕ;
ЃЈIIЃЉЧѓКЏЪ§![]() ЕФМЋжЕ;
ЕФМЋжЕ;
ЃЈIIIЃЉЕБ![]() ЪБ,ШєжБЯп
ЪБ,ШєжБЯп![]() гыЧњЯп
гыЧњЯп![]() УЛгаЙЋЙВЕу,Чѓ
УЛгаЙЋЙВЕу,Чѓ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§![]() .
.
(Ђё) ШєКЏЪ§![]() гаСуЕу, ЧѓЪЕЪ§
гаСуЕу, ЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇ;
ЕФШЁжЕЗЖЮЇ;
(Ђђ) жЄУї:ЕБ![]() ЪБ,
ЪБ, ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() ЪЧЖЈвхдк
ЪЧЖЈвхдк![]() ЩЯЕФЦцКЏЪ§ЃЌЕБ
ЩЯЕФЦцКЏЪ§ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ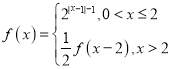 ЃЌдђ
ЃЌдђ![]() ЃЌдк
ЃЌдк![]() ЩЯЫљгаСуЕужЎКЭЮЊЃЈ ЃЉ
ЩЯЫљгаСуЕужЎКЭЮЊЃЈ ЃЉ
A.7 B.8 C.9 D.10
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЪ§Са{an}ЕФЧАnЯюКЭЮЊSnЃЌЧвТњзуa1=2ЃЌSn-4Sn-1-2=0ЃЈnЁн2ЃЌnЁЪZЃЉЃЎ
ЃЈЂёЃЉЧѓЪ§Са{an}ЕФЭЈЯюЙЋЪНЃЛ
ЃЈЂђЃЉСюbn=log2anЃЌTnЮЊ{bn}ЕФЧАnЯюКЭЃЌЧѓжЄ![]() ЃМ2ЃЎ
ЃМ2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМзЁЂввСНЖгВЮМгЬ§ИшВТИшУћгЮЯЗЃЌУПЖг3ШЫЃЎЫцЛњВЅЗХвЛЪзИшЧњЃЌВЮШќепПЊЪМЧРД№ЃЌУПШЫжЛгавЛДЮЧРД№ЛњЛсЃЈУПШЫЧРД№ЛњЛсОљЕШЃЉЃЌД№ЖдепЮЊБОЖггЎЕУвЛЗжЃЌД№ДэЕУСуЗжЃЎМйЩшМзЖгжаУПШЫД№ЖдЕФИХТЪОљЮЊ ![]() ЃЌввЖгжа3ШЫД№ЖдЕФИХТЪЗжБ№ЮЊ
ЃЌввЖгжа3ШЫД№ЖдЕФИХТЪЗжБ№ЮЊ ![]() ЃЌ
ЃЌ ![]() ЃЌ
ЃЌ ![]() ЃЌЧвИїШЫЛиД№е§ШЗгыЗёЯрЛЅжЎМфУЛгагАЯьЃЎ
ЃЌЧвИїШЫЛиД№е§ШЗгыЗёЯрЛЅжЎМфУЛгагАЯьЃЎ
ЃЈЂёЃЉШєБШШќЧАЫцЛњДгСНЖгЕФ6ИібЁЪжжаГщШЁСНУћбЁЪжНјааЪОЗЖЃЌЧѓГщЕНЕФСНУћбЁЪждкЭЌвЛИіЖгЕФИХТЪЃЛ
ЃЈЂђЃЉгУІЮБэЪОМзЖгЕФзмЕУЗжЃЌЧѓЫцЛњБфСПІЮЕФЗжВМСаКЭЪ§бЇЦкЭћЃЛ
ЃЈЂѓЃЉЧѓСНЖгЕУЗжжЎКЭДѓгк4ЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПКЏЪ§fЃЈxЃЉЖдвЛЧаЪЕЪ§xЃЌyОљгаfЃЈx+yЃЉЉfЃЈyЃЉ=ЃЈx+2y+2ЃЉxГЩСЂЃЌЧвfЃЈ2ЃЉ=12ЃЎ
ЃЈ1ЃЉЧѓfЃЈ0ЃЉЕФжЕЃЛ
ЃЈ2ЃЉдкЃЈ1ЃЌ4ЃЉЩЯДцдкx0ЁЪRЃЌЪЙЕУfЃЈx0ЃЉЉ8=ax0ГЩСЂЃЌЧѓЪЕЪ§aЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com