
 在某种产品表面进行腐蚀性试验,得到腐蚀深度y与腐蚀时间x之间对应的一组数据:
在某种产品表面进行腐蚀性试验,得到腐蚀深度y与腐蚀时间x之间对应的一组数据:| 时间x(s) | 2 | 3 | 4 | 5 | 6 |
| 深度y(μm) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
分析 (1)由已知中腐蚀深度y与腐蚀时间x之间的统计表中数据,易画出数据的散点图;
(2)根据所给的样本中心点和两个最小二乘法要用的和式,写出b的表示式,求出结果,再代入样本中心点求出a,写出线性回归方程;
(3)根据(2)中所得的线性回归方程,代入x=12求出预报值.
解答 解:(1)表中数据的散点图如下图所示: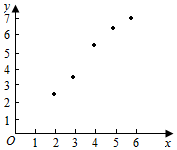
(2)$\overline x=4$,$\overline y=5$,
∴$\hat b=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}=\frac{112•3-100}{90-80}=1.23$,
$\hat a=\overline y-\hat b\overline x=5-1.23×4=0.08$
所以回归直线方程是:y=1.23x+0.08
(3)当x=12时,y=1.23×12+0.08=14.84μm
点评 本题考查线性回归方程的做法和应用,是一个基础题,本题解题的关键是正确应用最小二乘法来求线性回归方程的系数.


科目:高中数学 来源: 题型:解答题
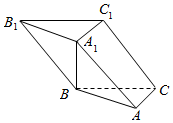 如图,在斜三棱柱ABC-A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.
如图,在斜三棱柱ABC-A1B1C1中,A1B⊥AC,且A1B=AC=5,AA1=BC=13,且AB=12.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
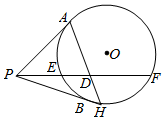 已知点P是圆O外的一点,过P作圆O的切线PA,PB,切点为A,B,过P作一割线交圆O于点E,F,若2PA=PF,取PF的中点D,连接AD,并延长交圆于H.
已知点P是圆O外的一点,过P作圆O的切线PA,PB,切点为A,B,过P作一割线交圆O于点E,F,若2PA=PF,取PF的中点D,连接AD,并延长交圆于H.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
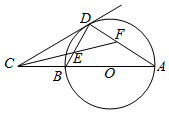 如图,AB是圆O的直径,C为AB的延长线上一点,切线CD交圆O于点D,∠ACD的平分线分别交DB,DA于点E,F.
如图,AB是圆O的直径,C为AB的延长线上一点,切线CD交圆O于点D,∠ACD的平分线分别交DB,DA于点E,F.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 使用年限x (年) | 2 | 3 | 4 | 5 | 6 |
| 维修费用y(万元) | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 价格x | 9 | 9.5 | 10.5 | 11 |
| 销售量y | 11 | 10 | 6 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
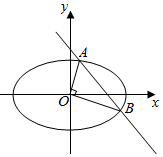 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2$\sqrt{3}$,长轴长为4.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的焦距为2$\sqrt{3}$,长轴长为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com