
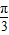 且R1=36cm,由此算出r1、r2和圆台的高h,结合圆台体积公式即可算出该圆台的体积.
且R1=36cm,由此算出r1、r2和圆台的高h,结合圆台体积公式即可算出该圆台的体积. αR22=
αR22= α•722,扇形OCD的面积S1=
α•722,扇形OCD的面积S1= αR12
αR12 α(722-R12)=648πcm2,可得
α(722-R12)=648πcm2,可得 α(72+R1)(72-R1)=648πcm2…(1)
α(72+R1)(72-R1)=648πcm2…(1)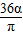 ,r1=
,r1=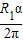 ,可得
,可得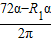 =6,整理得
=6,整理得 α(72-R1)=6π…(2)
α(72-R1)=6π…(2)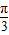 ,
,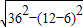 =6
=6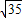
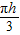 (r12+r1r2+r22)=
(r12+r1r2+r22)=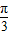 ×6
×6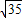 (62+6×12+122)=504
(62+6×12+122)=504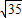 πcm2.
πcm2.

科目:高中数学 来源:高三数学教学与测试 题型:022
将半径为72cm的扇形OAB剪去一个扇形OCD,余下的扇环ABCD的面积为648π ,围成一圆台,圆台的下底与上底半径之差是6cm,则圆台的上底半径是________,下底半径是________,高是________.
,围成一圆台,圆台的下底与上底半径之差是6cm,则圆台的上底半径是________,下底半径是________,高是________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com