
【题目】设函数![]() ,其中
,其中![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)讨论函数![]() 的单调性;
的单调性;
(3)当![]() ,且
,且![]() 时,证明不等式
时,证明不等式![]() .
.
【答案】(1)![]() .(2)见解析(3)见解析
.(2)见解析(3)见解析
【解析】
(1)求导后求出斜率,点斜式即可求出答案;
(2)求导得 ,分
,分![]() 和
和![]() 讨论,借助导数即可求出单调性;
讨论,借助导数即可求出单调性;
(3)当![]() 时,
时,![]() ,令
,令![]()
![]() ,利用导数可得函数
,利用导数可得函数![]() 在区间
在区间![]() 上单调递增,得
上单调递增,得![]() 时,
时,![]() ,对任意正整数
,对任意正整数![]() ,取
,取![]() ,有
,有![]() ,利用裂项相消法即可证明.
,利用裂项相消法即可证明.
解:(1)当![]() 时,
时,![]() ,
,
∴![]() ,故切线的斜率为2,
,故切线的斜率为2,
∴函数![]() 的图象在点
的图象在点![]() 处的切线方程为
处的切线方程为![]() ;
;
(2)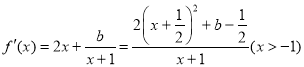 ,
,
当![]() 时,
时,![]() ,函数
,函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
当![]() 时,
时,![]() ,解得
,解得![]() ,
,![]() ,
,
①当![]() 时,
时,![]() ,
,![]() ,
,
令![]() ,解得
,解得![]() ,令
,令![]() ,解得
,解得![]() ,
,
∴函数![]() 在区间
在区间 上单调递减,在
上单调递减,在 上单调递增,
上单调递增,
②当![]() 时,
时,![]() ,
,
令![]() ,解得
,解得![]() 或
或![]() ,令
,令![]() ,解得
,解得![]() ,
,
∴函数![]() 在区间
在区间 上单调递减,
上单调递减,
在 ,
, 上单调递增;
上单调递增;
(3)证明:当![]() 时,
时,![]() ,
,
令![]() ,
,
![]() 在区间
在区间![]() 上恒为正,
上恒为正,
∴函数![]() 在区间
在区间![]() 上单调递增,
上单调递增,
当![]() )时,
)时,![]() ,
,
∴当![]() 时,
时,![]() ,
,
即![]() ,对任意正整数
,对任意正整数![]() ,取
,取![]() ,有
,有![]() ,
,
∴![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.


科目:高中数学 来源: 题型:
【题目】一个口袋内有![]() 个不同的红球,
个不同的红球,![]() 个不同的白球,
个不同的白球,
(1)从中任取![]() 个球,红球的个数不比白球少的取法有多少种?
个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记![]() 分,取一个白球记
分,取一个白球记![]() 分,从中任取
分,从中任取![]() 个球,使总分不少于
个球,使总分不少于![]() 分的取法有多少种?
分的取法有多少种?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=(x+1)ln x-2x.
(1)求函数的单调区间;
(2)设h(x)=f′(x)+![]() ,若h(x)>k(k∈Z)恒成立,求k的最大值.
,若h(x)>k(k∈Z)恒成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某射击运动员在比赛前进行三周的封闭训练,教练员将其每天成绩的均值数据整理,并绘成条形图如下,
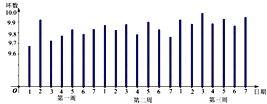
根据该图,下列说法错误的是:( )
A.第三周平均成绩最好B.第一周平均成绩比第二平均成绩好
C.第一周成绩波动较大D.第三周成绩比较稳定
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某周末,郑州方特梦幻王国汇聚了八方来客.面对该园区内相邻的两个主题公园“千古蝶恋”和“西游传说”,成年人和未成年人选择游玩的意向会有所不同.某统计机构对园区内的100位游客(这些游客只在两个主题公园中二选一)进行了问卷调查.调查结果显示,在被调查的50位成年人中,只有10人选择“西游传说”,而选择“西游传说”的未成年人有20人.
(1)根据题意,请将下面的![]() 列联表填写完整;
列联表填写完整;
选择“西游传说” | 选择“千古蝶恋” | 总计 | |
成年人 | |||
未成年人 | |||
总计 |
(2)根据列联表的数据,判断是否有![]() 的把握认为选择哪个主题公园与年龄有关.
的把握认为选择哪个主题公园与年龄有关.
附参考公式与表: (
(![]() ).
).
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R的奇函数![]() 满足
满足![]() ,且
,且![]() 时,
时, ![]() ,下面四种说法①
,下面四种说法①![]() ;②函数
;②函数![]() 在[-6,-2]上是增函数;③函数
在[-6,-2]上是增函数;③函数![]() 关于直线
关于直线![]() 对称;④若
对称;④若![]() ,则关于
,则关于![]() 的方程
的方程![]() 在[-8,8]上所有根之和为-8,其中正确的序号__________。
在[-8,8]上所有根之和为-8,其中正确的序号__________。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以直角坐标系的原点
为参数).以直角坐标系的原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立坐标系,曲线
轴的正半轴为极轴建立坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)若过点![]() 的直线
的直线![]() 与
与![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com