
 x2-
x2-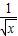 )n的展开式中,第9项为常数项,求:
)n的展开式中,第9项为常数项,求: x2-
x2-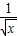 )n的展开式中,第9项为常数项,而第9项的通项公式为 T9=28-n•
)n的展开式中,第9项为常数项,而第9项的通项公式为 T9=28-n•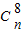 •x2n-20,故有 2n-20=0,由此解得 n=10.
•x2n-20,故有 2n-20=0,由此解得 n=10.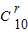 •
•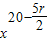 .令x的幂指数等于5,求得r的值,可得展开式中x5的系数.
.令x的幂指数等于5,求得r的值,可得展开式中x5的系数.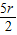 为整数,可得r=0,2,4,6,8,从而得到含x的整数次幂的项的个数.
为整数,可得r=0,2,4,6,8,从而得到含x的整数次幂的项的个数. x2-
x2- )n的展开式中,第9项为常数项,而第9项的通项公式为 T9=
)n的展开式中,第9项为常数项,而第9项的通项公式为 T9=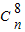 •28-n•x2n-16•x-4=28-n•
•28-n•x2n-16•x-4=28-n•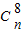 •x2n-20,
•x2n-20,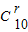 •2r-10•x20-2r•(-1)r•
•2r-10•x20-2r•(-1)r•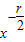 =(-1)r•2r-10•
=(-1)r•2r-10•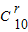 •
•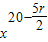 .
.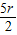 =5,求得r=6,故展开式中x5的系数为
=5,求得r=6,故展开式中x5的系数为 •
•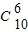 =
=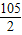 .
. 为整数,可得r=0,2,4,6,8,故含x的整数次幂的项的个数为5.
为整数,可得r=0,2,4,6,8,故含x的整数次幂的项的个数为5.

科目:高中数学 来源: 题型:
| x2-mx+1 | x |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| x2-mx+1 |
| x |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省济宁市高二(下)期末数学试卷(理科)(解析版) 题型:解答题
 x2-
x2-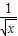 )n的展开式中,第9项为常数项,求:
)n的展开式中,第9项为常数项,求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com