
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,平面
,平面![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() 为等腰直角三角形,
为等腰直角三角形,![]() .
.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若三棱锥![]() 的体积为
的体积为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 上一点
上一点![]() 到其焦点F的距离为5.
到其焦点F的距离为5.
(1)求抛物线C的方程;
(2)设直线l与抛物线C交于A、B两点,O为坐标原点,若![]() ,求证:直线l必过一定点,并求出该定点的坐标;
,求证:直线l必过一定点,并求出该定点的坐标;
(3)过点![]() 的直线m与抛物线C交于不同的两点M、N,若
的直线m与抛物线C交于不同的两点M、N,若![]() ,求直线m的斜率的取值范围.
,求直线m的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
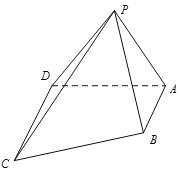
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]()
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为![]() ,求该四棱锥的侧面积.
,求该四棱锥的侧面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形PBCD中, ![]() ,A为PD的中点,如下左图。将
,A为PD的中点,如下左图。将![]() 沿AB折到
沿AB折到![]() 的位置,使
的位置,使![]() ,点E在SD上,且
,点E在SD上,且![]() ,如下图。
,如下图。
(1)求证: ![]() 平面ABCD;
平面ABCD;
(2)求二面角E—AC—D的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】邗江中学高二年级某班某小组共10人,利用寒假参加义工活动,已知参加义工活动次数为1,2,3的人数分别为3,3,4.现从这10人中选出2人作为该组代表参加座谈会.
(1)记“选出2人参加义工活动的次数之和为4”为事件![]() ,求事件
,求事件![]() 发生的概率;
发生的概率;
(2)设![]() 为选出2人参加义工活动次数之差的绝对值,求随机变量
为选出2人参加义工活动次数之差的绝对值,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学家欧拉在1765年提出:三角形的外心、重心位于同一直线上,这条直线被后人称之为三角形的欧拉线,若![]() 的顶点
的顶点![]() ,
,![]() ,且
,且![]() 的欧拉线的方程为
的欧拉线的方程为![]() .
.
(1)求![]() 外心
外心![]() (外接圆圆心)的坐标;
(外接圆圆心)的坐标;
(2)求顶点![]() 的坐标.
的坐标.
(注:如果![]() 三个顶点坐标分别为
三个顶点坐标分别为![]() ,
,![]() ,
,![]() ,则
,则![]() 重心的坐标是
重心的坐标是![]() .)
.)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com