
已知函数f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12和直线m:y=kx+9,且f′(-1)=0.
(1)求a的值.
(2)是否存在k的值,使直线m既是曲线y=f(x)的切线,又是曲线y=g(x)的切线?如果存在,求出k的值;如果不存在,说明理由.
(1) a=-2 (2) 公切线是y=9,此时k=0
【解析】(1)f'(x)=3ax2+6x-6a,f'(-1)=0,
即3a-6-6a=0,∴a=-2.
(2)存在.∵直线m恒过定点(0,9),直线m是曲线y=g(x)的切线,设切点为(x0,3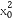 +6x0+12),
+6x0+12),
∵g'(x0)=6x0+6,
∴切线方程为y-(3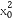 +6x0+12)=(6x0+6)(x-x0),将点(0,9)代入,得x0=±1,
+6x0+12)=(6x0+6)(x-x0),将点(0,9)代入,得x0=±1,
当x0=-1时,切线方程为y=9;
当x0=1时,切线方程为y=12x+9.
由f'(x)=0得-6x2+6x+12=0,
即有x=-1或x=2,
当x=-1时,y=f(x)的切线方程为y=-18;
当x=2时,y=f(x)的切线方程为y=9.
∴公切线是y=9.
又令f'(x)=12得-6x2+6x+12=12,
∴x=0或x=1.
当x=0时,y=f(x)的切线方程为y=12x-11;
当x=1时,y=f(x)的切线方程为y=12x-10,
∴公切线不是y=12x+9.
综上所述公切线是y=9,此时k=0.


科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十六第二章第十三节练习卷(解析版) 题型:填空题
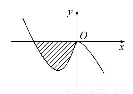
已知函数f(x)=-x3+ax2+bx(a,b∈R)的图象如图所示,它与x轴在原点处相切,且x轴与函数图象所围区域(图中阴影部分)的面积为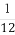 ,则a的值为 .
,则a的值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十二第二章第九节练习卷(解析版) 题型:解答题
某投资公司投资甲、乙两个项目所获得的利润分别是P(亿元)和Q(亿元),它们与投资额t(亿元)的关系有经验公式P=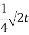 ,Q=
,Q= t,今该公司将5亿元投资于这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).求:
t,今该公司将5亿元投资于这两个项目,其中对甲项目投资x(亿元),投资这两个项目所获得的总利润为y(亿元).求:
(1)y关于x的函数表达式.
(2)总利润的最大值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十九第三章第三节练习卷(解析版) 题型:选择题
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)满足条件f(x+ )+f(x)=0,则ω的值为( )
)+f(x)=0,则ω的值为( )
(A)2π (B)π (C)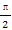 (D)
(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十三第二章第十节练习卷(解析版) 题型:填空题
设a>0,f(x)=ax2+bx+c,曲线y=f(x)在点P(x0,f(x0))处切线的倾斜角的取值范围为[0, ],则点P到曲线y=f(x)的对称轴的距离的取值范围为 .
],则点P到曲线y=f(x)的对称轴的距离的取值范围为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十三第二章第十节练习卷(解析版) 题型:选择题
函数y=cos(2x+1)的导数是( )
(A)y′=sin(2x+1)
(B)y′=-2xsin(2x+1)
(C)y′=-2sin(2x+1)
(D)y′=2xsin(2x+1)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业十一第二章第八节练习卷(解析版) 题型:解答题
已知函数f(x)=4x+m·2x+1有且仅有一个零点,求m的取值范围,并求出该零点.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业六十四第十章第一节练习卷(解析版) 题型:选择题
将3张不同的奥运会门票分给10名同学中的3人,每人1张,则不同的分法种数有( )
(A)2 160 (B)720 (C)240 (D)120
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com