
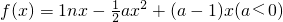
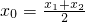 ,使得f′(x0)=k,请说明理由.
,使得f′(x0)=k,请说明理由. -ax+(a-1)=
-ax+(a-1)=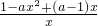 =
=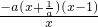 (x>0),
(x>0), >1,当0<x<1或x>-
>1,当0<x<1或x>- 时,f′(x)>0,f(x)单调递增;
时,f′(x)>0,f(x)单调递增; 时,f′(x)<0,f(x)单调递减.
时,f′(x)<0,f(x)单调递减. =1,此时,f′(x)≥0,f(x)在(0,+∞)上单调递增.
=1,此时,f′(x)≥0,f(x)在(0,+∞)上单调递增. <1,当0<x<-
<1,当0<x<- 或x>1时,f′(x)>0,f(x)单调递增;
或x>1时,f′(x)>0,f(x)单调递增; <x<1时,f′(x)<0,f(x)单调递减.
<x<1时,f′(x)<0,f(x)单调递减. ,+∞),减区间是(1,-
,+∞),减区间是(1,- );
); ),(1,+∞),减区间是(-
),(1,+∞),减区间是(- ,1).
,1).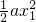 +(a-1)x1,
+(a-1)x1, ,
, =
= ,
, -
- (x2+x1)+(a-1),
(x2+x1)+(a-1), )=
)= -a•
-a• +(a-1),
+(a-1), )=
)= -a•
-a• +(a-1)=
+(a-1)= -
- (x2+x1)+(a-1),
(x2+x1)+(a-1), =
= ,即ln
,即ln =
=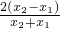 =
= ,
,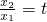 (t>1),上式化为lnt=
(t>1),上式化为lnt=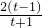 =2-
=2- ,
, =2,令g(t)=lnt+
=2,令g(t)=lnt+ ,g′(t)=
,g′(t)= -
-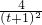 =
= ,
, =2成立,
=2成立,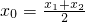 ,使得f′(x0)=k.
,使得f′(x0)=k. )=
)= -a•
-a• +(a-1)=
+(a-1)= -
- (x2+x1)+(a-1),化简然后构造函数,转化为函数的值域问题可判断.
(x2+x1)+(a-1),化简然后构造函数,转化为函数的值域问题可判断.

科目:高中数学 来源: 题型:
| π |
| 2 |
| 1 |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 12 |
| π |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2008-2009学年湖北省仙桃一中高三(上)第二次段考数学试卷(理科)(解析版) 题型:解答题


查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省枣庄市高三上学期期末检测理科数学 题型:解答题
(本题满分12分)
已知函数
(1)求函数 的极值点;
的极值点;
(2)若直线 过点(0,—1),并且与曲线
过点(0,—1),并且与曲线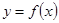 相切,求直线
相切,求直线 的方程;
的方程;
(3)设函数 ,其中
,其中 ,求函数
,求函数 在
在 上的最小值.(其中e为自然对数的底数)
上的最小值.(其中e为自然对数的底数)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com