
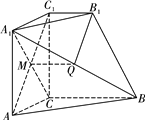
【题目】如图,在几何体![]() 中,平面
中,平面![]() 底面ABC,四边形
底面ABC,四边形![]() 是正方形,
是正方形,![]() ,Q是
,Q是![]() 的中点,且
的中点,且![]() ,
,![]() .
.

![]() 求证:
求证:![]() 平面
平面![]() ;
;
![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)连接![]() ,
,![]() 交于
交于![]() 点,连接
点,连接![]() ,则四边形
,则四边形![]() 是正方形,点
是正方形,点![]() 是
是![]() 的中点,推导出四边形
的中点,推导出四边形![]() 是平行四边形,从而
是平行四边形,从而![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
(2)以![]() 为原点,
为原点,![]() ,
,![]() 分别为
分别为![]() 轴和
轴和![]() 轴建立空间直角坐标系,利用向量法能求出二面角
轴建立空间直角坐标系,利用向量法能求出二面角![]() 的平面角的余弦值.
的平面角的余弦值.
证明:(1)如图所示,连接![]() ,
,![]() 交于
交于![]() 点,连接
点,连接![]() .
.
因为四边形![]() 是正方形,所以点
是正方形,所以点![]() 是
是![]() 的中点,
的中点,
又已知点![]() 是
是![]() 的中点,所以
的中点,所以![]() ,且
,且![]() ,
,
又因为![]() ,且
,且![]() ,所以
,所以![]() ,且
,且![]() ,
,
所以四边形![]() 是平行四边形,故
是平行四边形,故![]() ,
,
因![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.
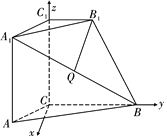
(2)如图所示,以![]() 为原点,
为原点,![]() 分别为
分别为![]() 轴和
轴和![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
不妨设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则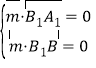 即
即![]() ,取
,取![]() ,则
,则![]()
平面![]() 的一个法向量
的一个法向量![]() ,所以
,所以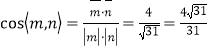 .
.
故二面角![]() 的平面角的余弦值为
的平面角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知圆![]() ,定点
,定点![]() ,
,![]() 为圆上任意一点,线段
为圆上任意一点,线段![]() 的垂直平分线
的垂直平分线![]() 和半径
和半径![]() 相交于点
相交于点![]() ,当点
,当点![]() 在圆上运动时,点
在圆上运动时,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若过定点![]() 的直线交曲线
的直线交曲线![]() 于不同的两点
于不同的两点![]() ,
,![]() (点
(点![]() 在点
在点![]() ,
,![]() 之间),且满足
之间),且满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对数函数g(x)=1ogax(a>0,a≠1)和指数函数f(x)=ax(a>0,a≠1)互为反函数.已知函数f(x)=3x,其反函数为y=g(x).
(Ⅰ)若函数g(kx2+2x+1)的定义域为R,求实数k的取值范围;
(Ⅱ)若0<x1<x2且|g(x1)|=|g(x2)|,求4x1+x2的最小值;
(Ⅲ)定义在I上的函数F(x),如果满足:对任意x∈I,总存在常数M>0,都有-M≤F(x)≤M成立,则称函数F(x)是I上的有界函数,其中M为函数F(x)的上界.若函数h(x)=![]() ,当m≠0时,探求函数h(x)在x∈[0,1]上是否存在上界M,若存在,求出M的取值范围,若不存在,请说明理由.
,当m≠0时,探求函数h(x)在x∈[0,1]上是否存在上界M,若存在,求出M的取值范围,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋中有4个大小相同的小球,其中红球1个,白球2个,黑球1个,现从袋中有放回地取球,每次随机取一个,求
(1)连续取两次都是白球的概率;
(2)若取一个红球记2分,取一个白球记1分,取一个黑球记0分,连续取三次分数之和为4分的概率.(本小题基本事件总数较多不要求列举,但是所求事件含的基本事件要列举)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】今天你低碳了吗?近来国内网站流行一种名为“碳排放计算器”的软件,人们可以由此计算出自己每天的碳排放量,如家居用电的碳排放量(千克)![]() 耗电度数
耗电度数![]() ,汽车的碳排放量(千克)
,汽车的碳排放量(千克)![]() 油耗公升数
油耗公升数![]() 等,某班同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查.若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这二族人数占各自小区总人数的比例
等,某班同学利用寒假在两个小区逐户进行了一次生活习惯是否符合低碳观念的调查.若生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,这二族人数占各自小区总人数的比例![]() 数据如下:
数据如下:
| 低碳族 | 非低碳族 |
| 低碳族 | 非低碳族 | |
比例 | 1/2 | 1/2 | 比例 | 4/5 | 1/5 |
(1)如果甲、乙来自![]() 小区,丙、丁来自
小区,丙、丁来自![]() 小区,求这4人中恰好有两人是低碳族的概率;
小区,求这4人中恰好有两人是低碳族的概率;
(2)![]() 小区经过大力宣传,每周非低碳中有20%的人加入到低碳族的行列,如果两周后随机地从
小区经过大力宣传,每周非低碳中有20%的人加入到低碳族的行列,如果两周后随机地从![]() 小区中任选5个人,记
小区中任选5个人,记![]() 表示5个人中的低碳族人数,求
表示5个人中的低碳族人数,求![]() 和
和![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某产品在3-7月份销售量与利润的统计数据如下表:
月份 | 3 | 4 | 5 | 6 | 7 |
销售量 | 3 | 6 | 4 | 7 | 8 |
利润 | 19 | 34 | 26 | 41 | 46 |
(1)从这5个月的利润中任选2个值,分别记为![]() ,求事件“
,求事件“![]() 均小于45”的概率;
均小于45”的概率;
(2)已知销售量![]() 与利润
与利润![]() 大致满足线性相关关系,请根据前4个月的数据,求出
大致满足线性相关关系,请根据前4个月的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的利润的估计数据与真实数据误差不超过2万元,则认为得到的利润估计是理想的.请用表格中7月份的数据检验由(2)中回归方程所得的该月的利润的估计数据是否理想?
参考公式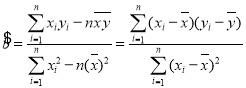 ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com