练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    （本小题满分12分）某租赁公司有汽车100辆,当每辆车月租金为3000元时,可全租出,当每辆车月租金每增加50元,未租出的车将会增加一辆.租出的车每辆每月需维护费150元,未租出的车每辆每月需维护费50元.
    (1)当每辆车月租金定为3600元时，能租出多少辆车？此时的月收益是多少？
    (2)每辆车的月租金定为多少元时，租赁公司的月收益最大？
    （12分） (1)  88辆  303000元
    (2) x=4050时，最大，最大值为.（元）.  
    （12分））解:(1)当每辆车的月租金定为3600元时，未租出的车辆数为，这时租出了88辆车.
    租赁公司的月收益为:（元）.………………4分
    (2)设每辆车的月租金定为x元，则租赁公司的月收益为

    ∴ 当x=4050时，最大，最大值为.（元）.        ……………………12分
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

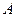    （本小题满分17分）某地政府招商引资,为吸引外商,决定第一年产品免税.某外资厂该年型产品出厂价为每件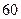元,年销售量为万件，第二年，当地政府开始对该商品征收税率为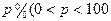，即销售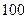元要征收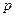元）的税收，于是该产品的出厂价上升为每件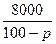元，预计年销售量将减少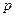万件．
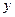    (1) 将第二年政府对该商品征收的税收(万元)表示成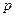的函数，并指出这个函数的定义域；
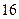    (2) 要使第二年该厂的税收不少于万元，则税率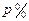的范围是多少？
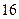    (3) 在第二年该厂的税收不少于万元的前提下，要让厂家获得最大销售金额，则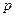应为多少？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （本题14分）
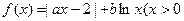    已知函数，实数a，b为常数），
    （1）若a＝1，在（0，＋∞）上是单调增函数，求b的取值范围；
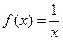    （2）若a≥2，b＝1，求方程在（0，1]上解的个数。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    函数与函数的交点为，则所在区间是（   ）
    A．B．C．D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    等腰三角形的周长是20，底边长y是一腰长x的函数，则y=f(x)等于(  )
    A．20-2x(0＜x≤10）B．20-2x(0＜x＜10)
    C．20-2x(5≤x≤10)D．20-2x(5＜x＜10)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知函数 若a，b，c均不相等，且，则的取值范围是
    A．（1，10）B．(5，6)C．(10，12)D．(20，24)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若函数f(x)=ex-2x-a在R上有两个零点，则实数a的取值范围是_________________．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知函数的定义域为，且，为的导函数，函数的图象如图所示，则不等式组所表示的平面区域的面积是（    ）
    A．3B．4C．5D．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    本小题９分
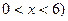    如图二某单位建造一间地面面积为12m2的背面靠墙的矩形小房，由于地理位置的限制，房子侧面的长度x（，房屋正面的造价为400元/m2,房屋侧面的造价为150元/m2，屋顶和地面的造价费用合计为5800元，如果墙高为3m，且不计房屋背面的费用
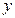    （1）把房屋总造价表示成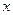的函数，并写出该函数的定义域。

    图二

     
    （2）当侧面的长度为多少时，总造价最底？最低总造价是多少？

     
    　　　　　　　　　　　　　　　

    查看答案和解析>>

    同步练习册答案