
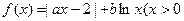 ,实数a,b为常数),
,实数a,b为常数), 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;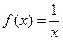 在(0,1]上解的个数。
在(0,1]上解的个数。科目:高中数学 来源:不详 题型:解答题
 一辆.
一辆. 租出的车每辆每月需维护费150元,未租出的车每辆每月需维护费50元.
租出的车每辆每月需维护费150元,未租出的车每辆每月需维护费50元.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
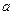 人,每人每年可创纯利润1万元.据评估,在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的
人,每人每年可创纯利润1万元.据评估,在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的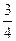 ,设该企业裁员
,设该企业裁员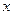 人后纯收益为
人后纯收益为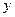 万元.
万元.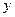 关于
关于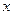 的函数关系式,并指出
的函数关系式,并指出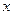 的取值范围;
的取值范围;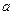 ≤280时,问企业裁员多少人,才能获得最大的经济效益?(注:在保证能获得最大经济效益的情况下,能少裁员,应尽量少裁)
≤280时,问企业裁员多少人,才能获得最大的经济效益?(注:在保证能获得最大经济效益的情况下,能少裁员,应尽量少裁)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com