
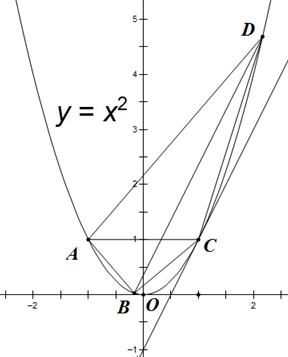
四边形ABCD的四个顶点都在抛物线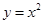 上,A,C关于
上,A,C关于 轴对称,BD平行于抛物线在点C处的切线。
轴对称,BD平行于抛物线在点C处的切线。
(Ⅰ)证明:AC平分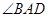 ;
;
(Ⅱ)若点A坐标为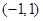 ,四边形ABCD的面积为4,求直线BD的方程。
,四边形ABCD的面积为4,求直线BD的方程。
(Ⅰ)详见解析;(Ⅱ)y=2x
【解析】
试题分析:(Ⅰ)依题意设出A、B、C、D四点的坐标,注意到AC的斜率为0,只需证AB、AD的斜率之和为0即可;(Ⅱ)四边形ABCD可以AC为底分成两个三角形求出面积,解出得到的方程即可.
试题解析:(Ⅰ)设A(x0, ),B(x1,
),B(x1, ),C(-x0,
),C(-x0, ),D(x2,
),D(x2,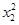 ).
).
对y=x2求导,得y¢=2x,则抛物线在点C处的切线斜率为-2x0.
直线BD的斜率k=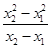 =x1+x2,
=x1+x2,
依题意,有x1+x2=-2x0.
记直线AB,AD的斜率分别为k1,k2,与BD的斜率求法同理,得
k1+k2=(x0+x1)+(x0+x2)=2x0+(x1+x2)=0,
所以∠CAB=∠CAD,即AC平分∠BAD.
(Ⅱ)由题设,x0=-1,x1+x2=2,k=2.四边形ABCD的面积
S=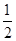 |AC|·
|AC|·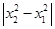 =
=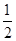 |AC|·|x2+x1|·|x2-x1|
|AC|·|x2+x1|·|x2-x1|
=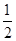 ×2×2×|2-2x1|=4|1-x1|,
×2×2×|2-2x1|=4|1-x1|,
由已知,4|1-x1|=4,得x1=0,或x1=2.
所以点B和D的坐标为(0,0)和(2,4),
故直线BD的方程为y=2x.
考点:1、抛物线及切线;2、直线的斜率及应用.


科目:高中数学 来源: 题型:
| 2 |
| 1 |
| 3 |
| A、空间四边形ABCD的四个顶点在同一球面上且此球的表面积为3π | ||
| B、空间四边形ABCD的四个顶点在同一球面上且此球的表面积为4π | ||
C、空间四边形ABCD的四个顶点在同一球上且此球的表面积为3
| ||
| D、不存在这样的球使得空间四边形ABCD的四个顶点在此球面上 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
(1)自圆O外一点P引切线与圆切于点A,M为PA中点,过M引割线交圆于B,C两点.求证:∠MCP=∠MPB.
|
| π |
| 6 |
| x |
| y |
| z |
| 1 | ||
|
| a2+b2+c2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com